Question-100815

Question Number 100815 by john santu last updated on 28/Jun/20

Answered by mr W last updated on 28/Jun/20

see Q47657 δ=(2+3+(√7))(−2+3+(√7))(2−3+(√7))(2+3−(√7)) =108 side length of equilateral triangle: l=(√((2^2 +3^2 +((√7))^2 +(√(3×108)))/2))=(√((20+18)/2))=(√(19)) cos α=((19+4−7)/(2×(√(19))×2))=((4(√(19)))/(19)) ⇒tan α=((√3)/4) cos β=((19+9−7)/(2×(√(19))×3))=((7(√(19)))/(38)) ⇒tan β=((3(√3))/7) tan (α+β)=((tan α+tan β)/(1−tan α tan β)) =((((√3)/4)+((3(√3))/7))/(1−((√3)/4)×((3(√3))/7)))=(√3) ⇒Answer A

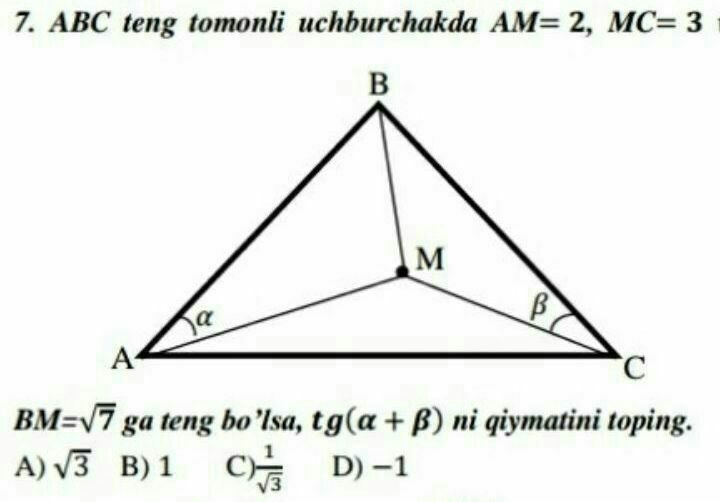
$${see}\:{Q}\mathrm{47657} \\ $$$$ \\ $$$$\delta=\left(\mathrm{2}+\mathrm{3}+\sqrt{\mathrm{7}}\right)\left(−\mathrm{2}+\mathrm{3}+\sqrt{\mathrm{7}}\right)\left(\mathrm{2}−\mathrm{3}+\sqrt{\mathrm{7}}\right)\left(\mathrm{2}+\mathrm{3}−\sqrt{\mathrm{7}}\right) \\ $$$$=\mathrm{108} \\ $$$${side}\:{length}\:{of}\:{equilateral}\:{triangle}: \\ $$$${l}=\sqrt{\frac{\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\left(\sqrt{\mathrm{7}}\right)^{\mathrm{2}} +\sqrt{\mathrm{3}×\mathrm{108}}}{\mathrm{2}}}=\sqrt{\frac{\mathrm{20}+\mathrm{18}}{\mathrm{2}}}=\sqrt{\mathrm{19}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{19}+\mathrm{4}−\mathrm{7}}{\mathrm{2}×\sqrt{\mathrm{19}}×\mathrm{2}}=\frac{\mathrm{4}\sqrt{\mathrm{19}}}{\mathrm{19}} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\mathrm{cos}\:\beta=\frac{\mathrm{19}+\mathrm{9}−\mathrm{7}}{\mathrm{2}×\sqrt{\mathrm{19}}×\mathrm{3}}=\frac{\mathrm{7}\sqrt{\mathrm{19}}}{\mathrm{38}} \\ $$$$\Rightarrow\mathrm{tan}\:\beta=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{7}} \\ $$$$\mathrm{tan}\:\left(\alpha+\beta\right)=\frac{\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta}{\mathrm{1}−\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta} \\ $$$$=\frac{\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}+\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{7}}}{\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}×\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{7}}}=\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{Answer}\:{A} \\ $$

Commented by bramlex last updated on 29/Jun/20