Question Number 100870 by bramlex last updated on 29/Jun/20

Commented by bemath last updated on 29/Jun/20
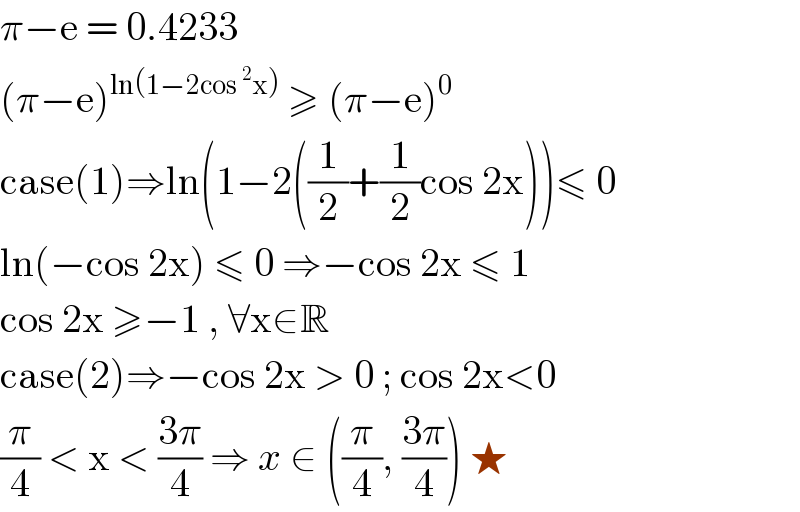
$$\pi−\mathrm{e}\:=\:\mathrm{0}.\mathrm{4233} \\ $$$$\left(\pi−\mathrm{e}\right)^{\mathrm{ln}\left(\mathrm{1}−\mathrm{2cos}\:^{\mathrm{2}} \mathrm{x}\right)} \:\geqslant\:\left(\pi−\mathrm{e}\right)^{\mathrm{0}} \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\Rightarrow\mathrm{ln}\left(\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2x}\right)\right)\leqslant\:\mathrm{0} \\ $$$$\mathrm{ln}\left(−\mathrm{cos}\:\mathrm{2x}\right)\:\leqslant\:\mathrm{0}\:\Rightarrow−\mathrm{cos}\:\mathrm{2x}\:\leqslant\:\mathrm{1} \\ $$$$\mathrm{cos}\:\mathrm{2x}\:\geqslant−\mathrm{1}\:,\:\forall\mathrm{x}\in\mathbb{R}\: \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\Rightarrow−\mathrm{cos}\:\mathrm{2x}\:>\:\mathrm{0}\:;\:\mathrm{cos}\:\mathrm{2x}<\mathrm{0} \\ $$$$\frac{\pi}{\mathrm{4}}\:<\:\mathrm{x}\:<\:\frac{\mathrm{3}\pi}{\mathrm{4}}\:\Rightarrow\:{x}\:\in\:\left(\frac{\pi}{\mathrm{4}},\:\frac{\mathrm{3}\pi}{\mathrm{4}}\right)\:\bigstar \\ $$
