Question Number 101001 by mhmd last updated on 29/Jun/20

Answered by mr W last updated on 29/Jun/20

Commented by mr W last updated on 29/Jun/20
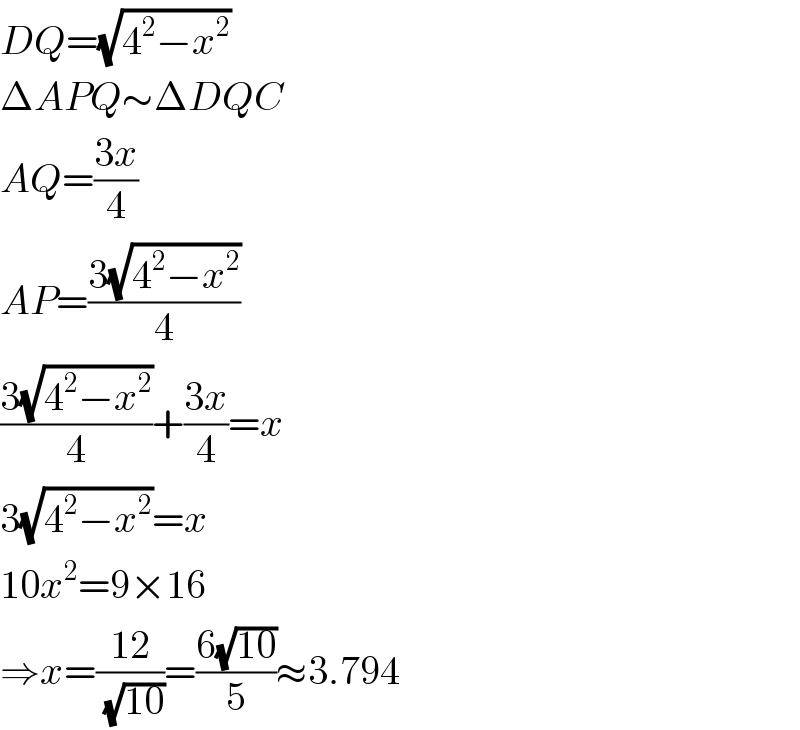
$${DQ}=\sqrt{\mathrm{4}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$\Delta{APQ}\sim\Delta{DQC} \\ $$$${AQ}=\frac{\mathrm{3}{x}}{\mathrm{4}} \\ $$$${AP}=\frac{\mathrm{3}\sqrt{\mathrm{4}^{\mathrm{2}} −{x}^{\mathrm{2}} }}{\mathrm{4}} \\ $$$$\frac{\mathrm{3}\sqrt{\mathrm{4}^{\mathrm{2}} −{x}^{\mathrm{2}} }}{\mathrm{4}}+\frac{\mathrm{3}{x}}{\mathrm{4}}={x} \\ $$$$\mathrm{3}\sqrt{\mathrm{4}^{\mathrm{2}} −{x}^{\mathrm{2}} }={x} \\ $$$$\mathrm{10}{x}^{\mathrm{2}} =\mathrm{9}×\mathrm{16} \\ $$$$\Rightarrow{x}=\frac{\mathrm{12}}{\:\sqrt{\mathrm{10}}}=\frac{\mathrm{6}\sqrt{\mathrm{10}}}{\mathrm{5}}\approx\mathrm{3}.\mathrm{794} \\ $$
