Question Number 101062 by bemath last updated on 30/Jun/20

Answered by MJS last updated on 30/Jun/20
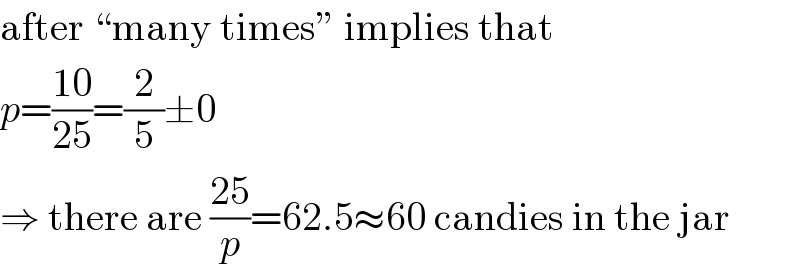
$$\mathrm{after}\:“\mathrm{many}\:\mathrm{times}''\:\mathrm{implies}\:\mathrm{that} \\ $$$${p}=\frac{\mathrm{10}}{\mathrm{25}}=\frac{\mathrm{2}}{\mathrm{5}}\pm\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{there}\:\mathrm{are}\:\frac{\mathrm{25}}{{p}}=\mathrm{62}.\mathrm{5}\approx\mathrm{60}\:\mathrm{candies}\:\mathrm{in}\:\mathrm{the}\:\mathrm{jar} \\ $$
Commented by bemath last updated on 30/Jun/20

$$\mathrm{sir}\:\mathrm{why}\:\frac{\mathrm{2}}{\mathrm{5}}\:\pm\:\mathrm{0}\:?\: \\ $$
Commented by bemath last updated on 30/Jun/20

$$\mathrm{how}\:\mathrm{sir}\:\mathrm{get}\:\mathrm{62}.\mathrm{5}\:? \\ $$
Commented by bemath last updated on 30/Jun/20
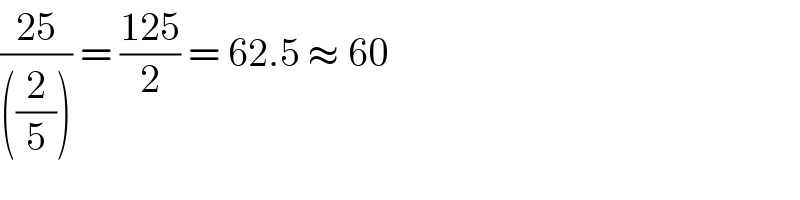
$$\frac{\mathrm{25}}{\left(\frac{\mathrm{2}}{\mathrm{5}}\right)}\:=\:\frac{\mathrm{125}}{\mathrm{2}}\:=\:\mathrm{62}.\mathrm{5}\:\approx\:\mathrm{60} \\ $$
Commented by MJS last updated on 30/Jun/20
![if we do not know the probability and we make one test as described here, we get a normally distributed p. we then have to define a confidence interval. usually you want to be at least 95% sure that the probability lies within [p−ε; p+ε] you′ll have to study this. but after “many tests” means we are 100% sure the probability is (2/5). then it′s easy: we marked 25 if we take out 25 we get 10 marked we must take out 2.5×25 to get 2.5×10 marked 2.5×25=62.5](https://www.tinkutara.com/question/Q101071.png)
$$\mathrm{if}\:\mathrm{we}\:\mathrm{do}\:\mathrm{not}\:\mathrm{know}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{and}\:\mathrm{we} \\ $$$$\mathrm{make}\:\mathrm{one}\:\mathrm{test}\:\mathrm{as}\:\mathrm{described}\:\mathrm{here},\:\mathrm{we}\:\mathrm{get}\:\mathrm{a} \\ $$$$\mathrm{normally}\:\mathrm{distributed}\:{p}.\:\mathrm{we}\:\mathrm{then}\:\mathrm{have}\:\mathrm{to} \\ $$$$\mathrm{define}\:\mathrm{a}\:\mathrm{confidence}\:\mathrm{interval}.\:\mathrm{usually}\:\mathrm{you} \\ $$$$\mathrm{want}\:\mathrm{to}\:\mathrm{be}\:\mathrm{at}\:\mathrm{least}\:\mathrm{95\%}\:\mathrm{sure}\:\mathrm{that}\:\mathrm{the} \\ $$$$\mathrm{probability}\:\mathrm{lies}\:\mathrm{within}\:\left[{p}−\epsilon;\:{p}+\epsilon\right] \\ $$$$\mathrm{you}'\mathrm{ll}\:\mathrm{have}\:\mathrm{to}\:\mathrm{study}\:\mathrm{this}. \\ $$$$\mathrm{but}\:\mathrm{after}\:“\mathrm{many}\:\mathrm{tests}''\:\mathrm{means}\:\mathrm{we}\:\mathrm{are}\:\mathrm{100\%} \\ $$$$\mathrm{sure}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{is}\:\frac{\mathrm{2}}{\mathrm{5}}.\:\mathrm{then}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}: \\ $$$$\mathrm{we}\:\mathrm{marked}\:\mathrm{25} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{take}\:\mathrm{out}\:\mathrm{25}\:\mathrm{we}\:\mathrm{get}\:\mathrm{10}\:\mathrm{marked} \\ $$$$\mathrm{we}\:\mathrm{must}\:\mathrm{take}\:\mathrm{out}\:\mathrm{2}.\mathrm{5}×\mathrm{25}\:\mathrm{to}\:\mathrm{get}\:\mathrm{2}.\mathrm{5}×\mathrm{10}\:\mathrm{marked} \\ $$$$\mathrm{2}.\mathrm{5}×\mathrm{25}=\mathrm{62}.\mathrm{5} \\ $$
Commented by bemath last updated on 30/Jun/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{for}\:\mathrm{your}\:\mathrm{explanation} \\ $$
