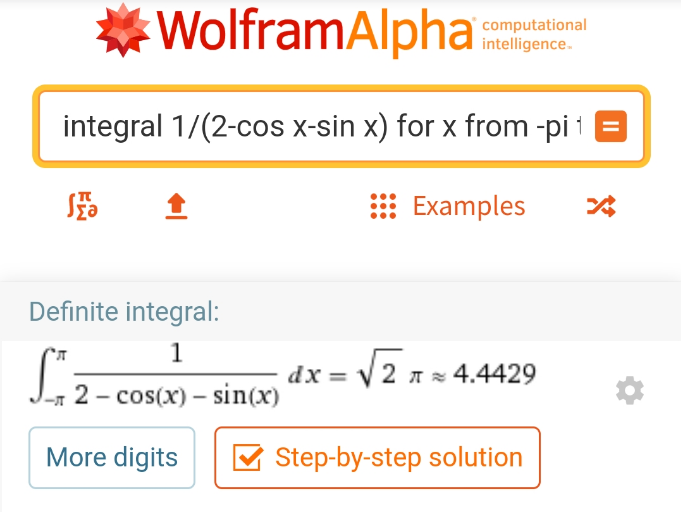
Question Number 101079 by I want to learn more last updated on 30/Jun/20

Commented by I want to learn more last updated on 30/Jun/20
$$\mathrm{Expecially}\:\mathrm{question}\:\left(\mathrm{2}\right)\:\mathrm{please} \\ $$
Commented by Dwaipayan Shikari last updated on 01/Jul/20
![∫_(−π) ^π (dx/(2−(((1−t^2 )/(1+t^2 ))+((2t)/(1+t^2 ))))) .(((1/2)sec^2 (x/2))/((1/2)sec^2 (x/2)))=2∫_(−π) ^π (dt/((1+t^2 )(((2+2t^2 −1+t^2 −2t)/(1+t^2 ))))) Suppose tanx=t and (dt/dx)=(1/2)sec^2 x and sec^2 (x/2)=1+t^2 =2∫_(−π) ^π (dt/(3t^2 −2t+1))=2∫_(−π) ^π (dt/((3t−(1/3))^2 +(((2(√2))/3))^2 ))=(2/3)∫_(−π) ^π (du/(u^2 +(((2(√2))/3))^2 )) =(2/3) (3/(2(√2)))tan^(−1) (((3u)/(2(√2))))=(√2)tan^(−1) (((9t−1)/(2(√2))))=[(√2)tan^(−1) (((9tan(x/2)−1)/(2(√2))))]_(−π) ^π suppose (3t−(1/3))=u =(√2)((π/2)+(π/2))=(√2)π★](https://www.tinkutara.com/question/Q101208.png)
$$\int_{−\pi} ^{\pi} \frac{{dx}}{\mathrm{2}−\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)}\:.\frac{\frac{\mathrm{1}}{\mathrm{2}}{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}=\mathrm{2}\int_{−\pi} ^{\pi} \frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\frac{\mathrm{2}+\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$${Suppose}\:{tanx}={t}\:\:{and}\:\frac{{dt}}{{dx}}=\frac{\mathrm{1}}{\mathrm{2}}{sec}^{\mathrm{2}} {x}\:\:\:{and}\:\:\:{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}=\mathrm{1}+{t}^{\mathrm{2}} \\ $$$$=\mathrm{2}\int_{−\pi} ^{\pi} \frac{{dt}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}}=\mathrm{2}\int_{−\pi} ^{\pi} \frac{{dt}}{\left(\mathrm{3}{t}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{3}}\int_{−\pi} ^{\pi} \frac{{du}}{{u}^{\mathrm{2}} +\left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}{u}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)=\sqrt{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{9}{t}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)=\left[\sqrt{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{9}{tan}\frac{{x}}{\mathrm{2}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)\right]_{−\pi} ^{\pi} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:{suppose}\:\left(\mathrm{3}{t}−\frac{\mathrm{1}}{\mathrm{3}}\right)={u} \\ $$$$\:\:\:\:\:\:\:=\sqrt{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)=\sqrt{\mathrm{2}}\pi\bigstar \\ $$
Answered by abdomathmax last updated on 01/Jul/20
![classic method A =∫_(−π) ^π (dx/(2−(cosx +sinx))) changement tan((x/2))=t give A =∫_(−∞) ^(+∞) ((2dt)/((1+t^2 ){2−(((1−t^2 )/(1+t^2 ))+((2t)/(1+t^2 )))})) =∫_(−∞) ^(+∞ ) ((2dt)/(2+2t^2 −1+t^2 −2t)) =∫_(−∞) ^(+∞) ((2dt)/(3t^2 −2t+1)) =(2/3) ∫_(−∞) ^(+∞) (dt/(t^2 −(2/3)t +(1/3))) =(2/3) ∫_(−∞) ^(+∞ ) (dt/(t^2 −(2/3)t +(1/9)+(1/3)−(1/9))) =(2/3) ∫_(−∞) ^(+∞) (dt/((t−(1/3))^2 +(2/9))) =_(t−(1/3)=((√2)/3)u) (2/3)×(9/2) ∫_(−∞) ^(+∞) (1/(u^2 +1))×((√2)/3) du =(√2)∫_(−∞) ^(+∞) (du/(1+u^2 )) =(√2)[ arctanu]_(−∞) ^(+∞) =(√2){(π/2)−(−(π/2))} =π(√2) ★A =π(√2)★](https://www.tinkutara.com/question/Q101160.png)
$$\mathrm{classic}\:\mathrm{method}\:\mathrm{A}\:=\int_{−\pi} ^{\pi} \:\frac{\mathrm{dx}}{\mathrm{2}−\left(\mathrm{cosx}\:+\mathrm{sinx}\right)} \\ $$$$\mathrm{changement}\:\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}\:\mathrm{give}\: \\ $$$$\mathrm{A}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left\{\mathrm{2}−\left(\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }+\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)\right\}} \\ $$$$=\int_{−\infty} ^{+\infty\:} \:\frac{\mathrm{2dt}}{\mathrm{2}+\mathrm{2t}^{\mathrm{2}} −\mathrm{1}+\mathrm{t}^{\mathrm{2}} −\mathrm{2t}}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{2dt}}{\mathrm{3t}^{\mathrm{2}} −\mathrm{2t}+\mathrm{1}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:\int_{−\infty} ^{+\infty} \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}\mathrm{t}\:+\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:\int_{−\infty} ^{+\infty\:} \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}\mathrm{t}\:+\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{9}}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dt}}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} \:+\frac{\mathrm{2}}{\mathrm{9}}} \\ $$$$=_{\mathrm{t}−\frac{\mathrm{1}}{\mathrm{3}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\mathrm{u}} \:\:\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{9}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}×\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\:\mathrm{du} \\ $$$$=\sqrt{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\:=\sqrt{\mathrm{2}}\left[\:\mathrm{arctanu}\right]_{−\infty} ^{+\infty} \\ $$$$=\sqrt{\mathrm{2}}\left\{\frac{\pi}{\mathrm{2}}−\left(−\frac{\pi}{\mathrm{2}}\right)\right\}\:=\pi\sqrt{\mathrm{2}} \\ $$$$\bigstar\mathrm{A}\:=\pi\sqrt{\mathrm{2}}\bigstar \\ $$
Commented by I want to learn more last updated on 02/Jul/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 30/Jun/20
![∫_(−π) ^π (dx/(2−(cos x+sin x))) =(1/( (√2)))∫_(−π) ^π (dx/( (√2)−cos (x−(π/4)))) =(1/( (√2)))∫_(−((5π)/4)) ^((3π)/4) (dt/( (√2)−cos t)) =(√2)[tan^(−1) {((√2)+1)tan (t/2)}]_(−((5π)/4)) ^(−π) +(√2)[tan^(−1) {((√2)+1)tan (t/2)}]_(−π) ^((3π)/4) =(√2)[(π/2)−tan^(−1) ((√2)+1)^2 +tan^(−1) ((√2)+1)^2 +(π/2)] =(√2)π](https://www.tinkutara.com/question/Q101132.png)
$$\int_{−\pi} ^{\pi} \frac{{dx}}{\mathrm{2}−\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{−\pi} ^{\pi} \frac{{dx}}{\:\sqrt{\mathrm{2}}−\mathrm{cos}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{−\frac{\mathrm{5}\pi}{\mathrm{4}}} ^{\frac{\mathrm{3}\pi}{\mathrm{4}}} \frac{{dt}}{\:\sqrt{\mathrm{2}}−\mathrm{cos}\:{t}} \\ $$$$=\sqrt{\mathrm{2}}\left[\mathrm{tan}^{−\mathrm{1}} \left\{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\mathrm{tan}\:\frac{{t}}{\mathrm{2}}\right\}\right]_{−\frac{\mathrm{5}\pi}{\mathrm{4}}} ^{−\pi} \\ $$$$\:\:\:\:\:+\sqrt{\mathrm{2}}\left[\mathrm{tan}^{−\mathrm{1}} \left\{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\mathrm{tan}\:\frac{{t}}{\mathrm{2}}\right\}\right]_{−\pi} ^{\frac{\mathrm{3}\pi}{\mathrm{4}}} \\ $$$$=\sqrt{\mathrm{2}}\left[\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} +\frac{\pi}{\mathrm{2}}\right] \\ $$$$=\sqrt{\mathrm{2}}\pi \\ $$
Commented by I want to learn more last updated on 30/Jun/20
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate} \\ $$
Commented by mr W last updated on 30/Jun/20