Question Number 101085 by ajfour last updated on 30/Jun/20

Commented by ajfour last updated on 30/Jun/20
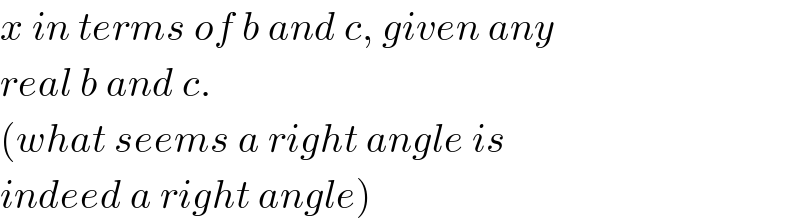
$${x}\:{in}\:{terms}\:{of}\:{b}\:{and}\:{c},\:{given}\:{any} \\ $$$${real}\:{b}\:{and}\:{c}. \\ $$$$\left({what}\:{seems}\:{a}\:{right}\:{angle}\:{is}\:\right. \\ $$$$\left.{indeed}\:{a}\:{right}\:{angle}\right) \\ $$
Answered by 1549442205 last updated on 07/Jul/20
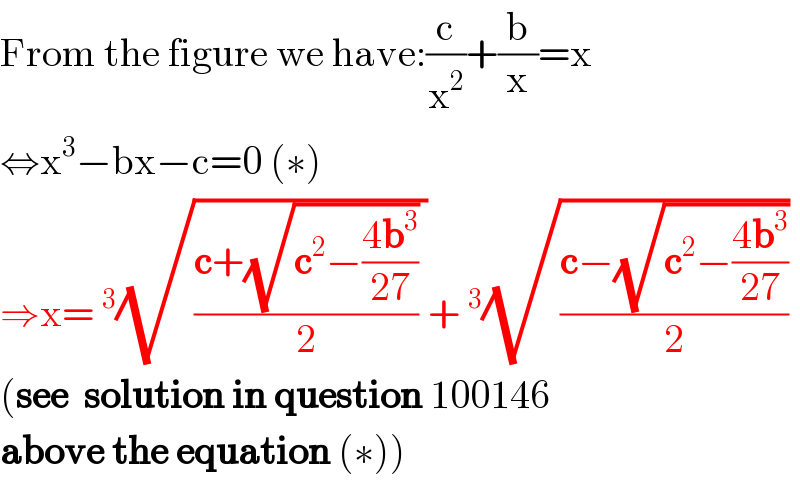
$$\mathrm{From}\:\mathrm{the}\:\mathrm{figure}\:\mathrm{we}\:\mathrm{have}:\frac{\mathrm{c}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{b}}{\mathrm{x}}=\mathrm{x} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{3}} −\mathrm{bx}−\mathrm{c}=\mathrm{0}\:\left(\ast\right) \\ $$$$\Rightarrow\mathrm{x}=\:^{\mathrm{3}} \sqrt{\frac{\boldsymbol{\mathrm{c}}+\sqrt{\boldsymbol{\mathrm{c}}^{\mathrm{2}} −\frac{\mathrm{4}\boldsymbol{\mathrm{b}}^{\mathrm{3}} }{\mathrm{27}}}}{\mathrm{2}}\:}+\:^{\mathrm{3}} \sqrt{\frac{\boldsymbol{\mathrm{c}}−\sqrt{\boldsymbol{\mathrm{c}}^{\mathrm{2}} −\frac{\mathrm{4}\boldsymbol{\mathrm{b}}^{\mathrm{3}} }{\mathrm{27}}}}{\mathrm{2}}} \\ $$$$\left(\boldsymbol{\mathrm{see}}\:\:\boldsymbol{\mathrm{solution}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{question}}\:\mathrm{100146}\:\right. \\ $$$$\left.\boldsymbol{\mathrm{above}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{equation}}\:\left(\ast\right)\right) \\ $$
