Question Number 101107 by PengagumRahasiamu last updated on 30/Jun/20
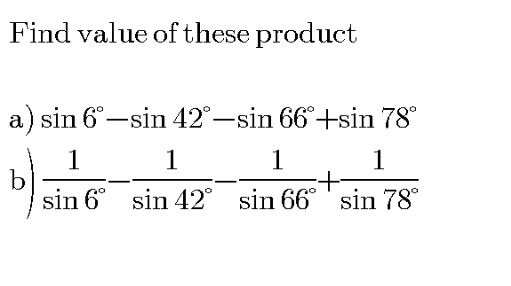
Commented by Dwaipayan Shikari last updated on 30/Jun/20
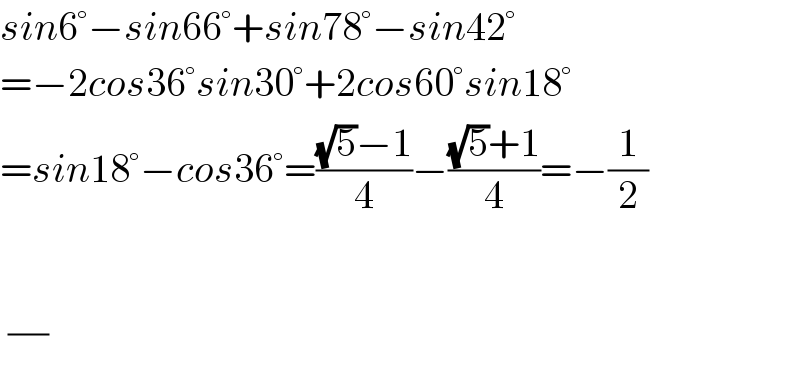
$${sin}\mathrm{6}°−{sin}\mathrm{66}°+{sin}\mathrm{78}°−{sin}\mathrm{42}° \\ $$$$=−\mathrm{2}{cos}\mathrm{36}°{sin}\mathrm{30}°+\mathrm{2}{cos}\mathrm{60}°{sin}\mathrm{18}° \\ $$$$={sin}\mathrm{18}°−{cos}\mathrm{36}°=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}−\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\:\frac{}{} \\ $$
Commented by Dwaipayan Shikari last updated on 01/Jul/20
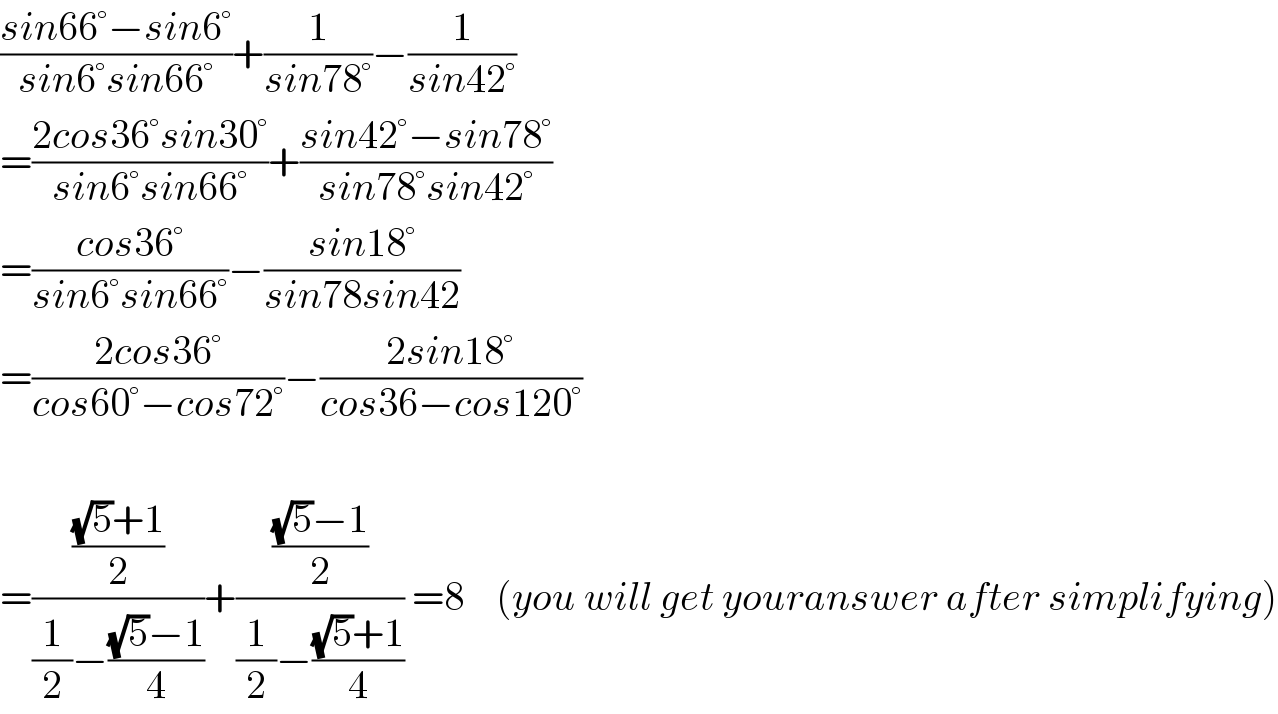
$$\frac{{sin}\mathrm{66}°−{sin}\mathrm{6}°}{{sin}\mathrm{6}°{sin}\mathrm{66}°}+\frac{\mathrm{1}}{{sin}\mathrm{78}°}−\frac{\mathrm{1}}{{sin}\mathrm{42}°} \\ $$$$=\frac{\mathrm{2}{cos}\mathrm{36}°{sin}\mathrm{30}°}{{sin}\mathrm{6}°{sin}\mathrm{66}°}+\frac{{sin}\mathrm{42}°−{sin}\mathrm{78}°}{{sin}\mathrm{78}°{sin}\mathrm{42}°} \\ $$$$=\frac{{cos}\mathrm{36}°}{{sin}\mathrm{6}°{sin}\mathrm{66}°}−\frac{{sin}\mathrm{18}°}{{sin}\mathrm{78}{sin}\mathrm{42}} \\ $$$$=\frac{\mathrm{2}{cos}\mathrm{36}°}{{cos}\mathrm{60}°−{cos}\mathrm{72}°}−\frac{\mathrm{2}{sin}\mathrm{18}°}{{cos}\mathrm{36}−{cos}\mathrm{120}°} \\ $$$$ \\ $$$$=\frac{\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}}+\frac{\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}}\:=\mathrm{8}\:\:\:\:\left({you}\:{will}\:{get}\:{youranswer}\:{after}\:{simplifying}\right) \\ $$
Answered by Ar Brandon last updated on 30/Jun/20
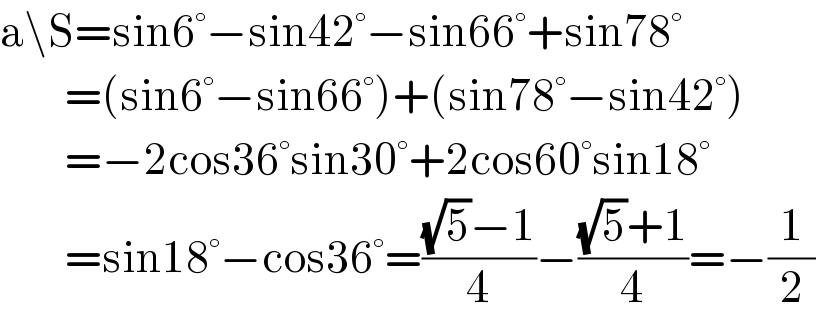
$$\mathrm{a}\backslash\mathrm{S}=\mathrm{sin6}°−\mathrm{sin42}°−\mathrm{sin66}°+\mathrm{sin78}° \\ $$$$\:\:\:\:\:\:\:\:=\left(\mathrm{sin6}°−\mathrm{sin66}°\right)+\left(\mathrm{sin78}°−\mathrm{sin42}°\right) \\ $$$$\:\:\:\:\:\:\:\:=−\mathrm{2cos36}°\mathrm{sin30}°+\mathrm{2cos60}°\mathrm{sin18}° \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{sin18}°−\mathrm{cos36}°=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}−\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by Ar Brandon last updated on 30/Jun/20
![b\T=(1/(sin6°))−(1/(sin66°))+(1/(sin78°))−(1/(sin42°))=((sin66°−sin6°)/(sin66°sin6°))+((sin42°−sin78°)/(sin42°sin78°)) =((2cos36°sin30°)/(((−1)/2)(cos72°−cos60°)))+((−2cos60°sin18°)/(((−1)/2)(cos120°−cos36°))) =((−2cos36°)/((sin18°−(1/2))))+((2sin18°)/((−(1/2)−cos36°)))=((−2∙((((√5)+1))/4))/(((((√5)−1)/4)−(1/2))))+((2∙(((√5)−1)/4))/((((−1)/2)−(((√5)+1)/4)))) =((−2((√5)+1))/( (√5)−1−2))+((2((√5)−1))/((−2−(√5)−1)))=((2((√5)+1))/(3−(√5)))+((2(1−(√5)))/(3+(√5))) =((2[(1+(√5))(3+(√5))+(1−(√5))(3−(√5))])/((3−(√5))(3+(√5))))=((2(8+4(√5)+8−4(√5)))/4) (1/(sin6°))−(1/(sin66°))+(1/(sin78°))−(1/(sin42°))=8](https://www.tinkutara.com/question/Q101113.png)
$$\mathrm{b}\backslash\mathrm{T}=\frac{\mathrm{1}}{\mathrm{sin6}°}−\frac{\mathrm{1}}{\mathrm{sin66}°}+\frac{\mathrm{1}}{\mathrm{sin78}°}−\frac{\mathrm{1}}{\mathrm{sin42}°}=\frac{\mathrm{sin66}°−\mathrm{sin6}°}{\mathrm{sin66}°\mathrm{sin6}°}+\frac{\mathrm{sin42}°−\mathrm{sin78}°}{\mathrm{sin42}°\mathrm{sin78}°} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2cos36}°\mathrm{sin30}°}{\frac{−\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos72}°−\mathrm{cos60}°\right)}+\frac{−\mathrm{2cos60}°\mathrm{sin18}°}{\frac{−\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos120}°−\mathrm{cos36}°\right)} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{−\mathrm{2cos36}°}{\left(\mathrm{sin18}°−\frac{\mathrm{1}}{\mathrm{2}}\right)}+\frac{\mathrm{2sin18}°}{\left(−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{cos36}°\right)}=\frac{−\mathrm{2}\centerdot\frac{\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\mathrm{4}}}{\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\right)}+\frac{\mathrm{2}\centerdot\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}}{\left(\frac{−\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{−\mathrm{2}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\:\sqrt{\mathrm{5}}−\mathrm{1}−\mathrm{2}}+\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)}{\left(−\mathrm{2}−\sqrt{\mathrm{5}}−\mathrm{1}\right)}=\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\mathrm{3}−\sqrt{\mathrm{5}}}+\frac{\mathrm{2}\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)}{\mathrm{3}+\sqrt{\mathrm{5}}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}\left[\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)+\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)\right]}{\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)}=\frac{\mathrm{2}\left(\mathrm{8}+\mathrm{4}\sqrt{\mathrm{5}}+\mathrm{8}−\mathrm{4}\sqrt{\mathrm{5}}\right)}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin6}°}−\frac{\mathrm{1}}{\mathrm{sin66}°}+\frac{\mathrm{1}}{\mathrm{sin78}°}−\frac{\mathrm{1}}{\mathrm{sin42}°}=\mathrm{8} \\ $$
Commented by PengagumRahasiamu last updated on 30/Jun/20
Thank you, Sir ����
Commented by Ar Brandon last updated on 30/Jun/20
You're welcome mate ! ��
