Question-101350

Question Number 101350 by bobhans last updated on 02/Jul/20

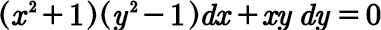
Answered by bemath last updated on 02/Jul/20

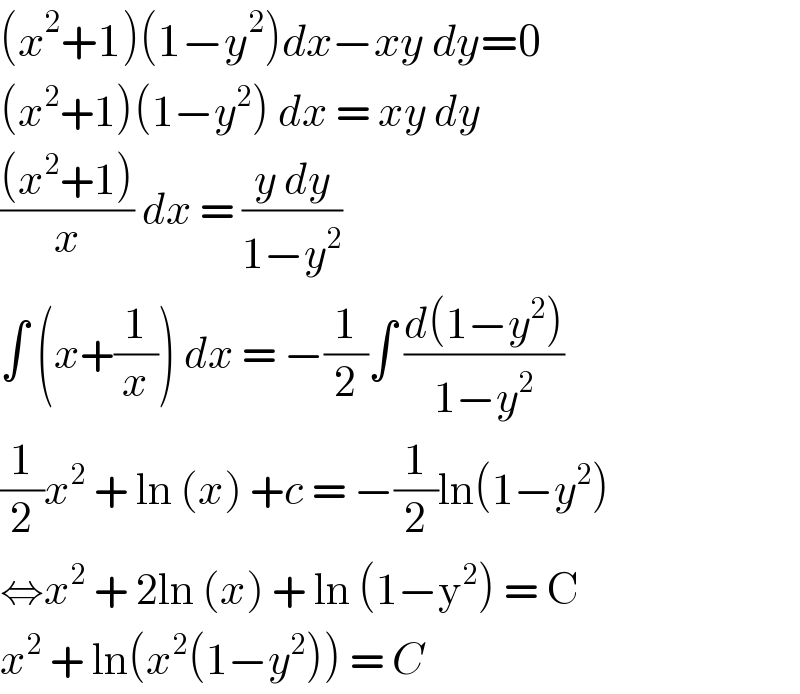
(x^2 +1)(1−y^2 )dx−xy dy=0 (x^2 +1)(1−y^2 ) dx = xy dy (((x^2 +1))/x) dx = ((y dy)/(1−y^2 )) ∫ (x+(1/x)) dx = −(1/2)∫ ((d(1−y^2 ))/(1−y^2 )) (1/2)x^2 + ln (x) +c = −(1/2)ln(1−y^2 ) ⇔x^2 + 2ln (x) + ln (1−y^2 ) = C x^2 + ln(x^2 (1−y^2 )) = C

$$\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{1}−{y}^{\mathrm{2}} \right){dx}−{xy}\:{dy}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{1}−{y}^{\mathrm{2}} \right)\:{dx}\:=\:{xy}\:{dy}\: \\ $$$$\frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{{x}}\:{dx}\:=\:\frac{{y}\:{dy}}{\mathrm{1}−{y}^{\mathrm{2}} } \\ $$$$\int\:\left({x}+\frac{\mathrm{1}}{{x}}\right)\:{dx}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{d}\left(\mathrm{1}−{y}^{\mathrm{2}} \right)}{\mathrm{1}−{y}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \:+\:\mathrm{ln}\:\left({x}\right)\:+{c}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}−{y}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow{x}^{\mathrm{2}} \:+\:\mathrm{2ln}\:\left({x}\right)\:+\:\mathrm{ln}\:\left(\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)\:=\:\mathrm{C} \\ $$$${x}^{\mathrm{2}} \:+\:\mathrm{ln}\left({x}^{\mathrm{2}} \left(\mathrm{1}−{y}^{\mathrm{2}} \right)\right)\:=\:{C}\: \\ $$

Commented by bobhans last updated on 02/Jul/20

$$\mathrm{yeahhh}..\bigstar\blacksquare \\ $$

Facebook Tweet Pin

Question-101350

Leave a Reply Cancel reply