Menu Close

Question-101382

Tinku Tara 0 Comments
Pin




Question Number 101382 by student work last updated on 02/Jul/20
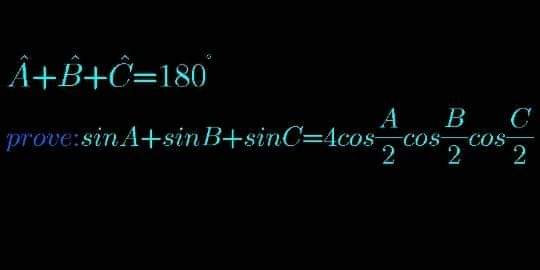
Answered by Rio Michael last updated on 02/Jul/20
we know or we are to prove that sin A + sinB + sin C = 4 cos(A/2) cos(B/2) cos(C/2) ((1) but A + B + C = π(180°) ⇒ A + B = π−C and ((A +B)/2) = ((π − C)/2) ⇒ ((A + B)/2) = (π/2)−(C/2) so sin (((A + B)/2)) = cos((π/2) −(C/2)) = cos ((C/2)) (2) also sin C = 2 sin ((C/2)) cos ((C/2))......(3) but sin A+ sin B + sinC = 2 cos((C/2))cos (((A − B)/2)) + 2 sin ((C/2)) cos((C/2)) = 2 cos ((C/2))[cos (((A − B)/2)) + sin ((C/2))] = 2 cos ((C/2))[cos (((A−B)/2)) + sin (((π−(A + B))/2))] since A + B + C = π = 2 cos((C/2))[cos (((A−B)/2)) + sin ((π/2)−((A + B)/2))] = 2 cos ((C/2))[cos (((A−B)/2)) + cos (((A + B)/2))] = 2 cos ((C/2))[2cos (((((A −B)/2) + ((A +B)/2))/2)) cos(((((A−B)/2)−((A +B)/2))/2))] = 2 cos ((C/2))[2cos((A/2))cos (−(B/2))] = 4 cos ((A/2))cos ((B/2)) cos ((C/2)) since cos x is an even function. QED
$$\mathrm{we}\:\mathrm{know}\:\mathrm{or}\:\mathrm{we}\:\mathrm{are}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{that}\:\:\mathrm{sin}\:{A}\:+\:\mathrm{sin}{B}\:+\:\mathrm{sin}\:{C}\:=\:\mathrm{4}\:\mathrm{cos}\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\frac{{B}}{\mathrm{2}}\:\mathrm{cos}\frac{{C}}{\mathrm{2}}\:\left(\left(\mathrm{1}\right)\right. \\ $$$$\mathrm{but}\:{A}\:+\:{B}\:+\:{C}\:=\:\pi\left(\mathrm{180}°\right) \\ $$$$\Rightarrow\:{A}\:+\:{B}\:=\:\pi−{C}\:\mathrm{and}\:\:\frac{{A}\:+{B}}{\mathrm{2}}\:=\:\frac{\pi\:−\:{C}}{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow\:\:\frac{{A}\:+\:{B}}{\mathrm{2}}\:=\:\frac{\pi}{\mathrm{2}}−\frac{{C}}{\mathrm{2}} \\ $$$$\mathrm{so}\:\mathrm{sin}\:\left(\frac{{A}\:+\:{B}}{\mathrm{2}}\right)\:=\:\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}\:−\frac{{C}}{\mathrm{2}}\right)\:\:=\:\mathrm{cos}\:\left(\frac{{C}}{\mathrm{2}}\right)\:\left(\mathrm{2}\right) \\ $$$$\mathrm{also}\:\mathrm{sin}\:{C}\:=\:\mathrm{2}\:\mathrm{sin}\:\left(\frac{{C}}{\mathrm{2}}\right)\:\mathrm{cos}\:\left(\frac{{C}}{\mathrm{2}}\right)……\left(\mathrm{3}\right) \\ $$$$\mathrm{but}\:\mathrm{sin}\:{A}+\:\mathrm{sin}\:{B}\:+\:\mathrm{sin}{C}\:\:=\:\mathrm{2}\:\mathrm{cos}\left(\frac{{C}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{A}\:−\:{B}}{\mathrm{2}}\right)\:+\:\mathrm{2}\:\mathrm{sin}\:\left(\frac{{C}}{\mathrm{2}}\right)\:\mathrm{cos}\left(\frac{{C}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:=\:\mathrm{2}\:\mathrm{cos}\:\left(\frac{{C}}{\mathrm{2}}\right)\left[\mathrm{cos}\:\left(\frac{{A}\:−\:{B}}{\mathrm{2}}\right)\:+\:\mathrm{sin}\:\left(\frac{{C}}{\mathrm{2}}\right)\right] \\ $$$$\:\:\:\:\:=\:\mathrm{2}\:\mathrm{cos}\:\left(\frac{{C}}{\mathrm{2}}\right)\left[\mathrm{cos}\:\left(\frac{{A}−{B}}{\mathrm{2}}\right)\:+\:\mathrm{sin}\:\left(\frac{\pi−\left({A}\:+\:{B}\right)}{\mathrm{2}}\right)\right]\:\:\mathrm{since}\:{A}\:+\:{B}\:+\:{C}\:=\:\pi \\ $$$$\:\:\:\:\:=\:\mathrm{2}\:\mathrm{cos}\left(\frac{{C}}{\mathrm{2}}\right)\left[\mathrm{cos}\:\left(\frac{{A}−{B}}{\mathrm{2}}\right)\:+\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\frac{{A}\:+\:{B}}{\mathrm{2}}\right)\right]\: \\ $$$$\:\:\:\:\:=\:\mathrm{2}\:\mathrm{cos}\:\left(\frac{{C}}{\mathrm{2}}\right)\left[\mathrm{cos}\:\left(\frac{{A}−{B}}{\mathrm{2}}\right)\:+\:\mathrm{cos}\:\left(\frac{{A}\:+\:{B}}{\mathrm{2}}\right)\right] \\ $$$$\:\:\:\:\:=\:\mathrm{2}\:\mathrm{cos}\:\left(\frac{{C}}{\mathrm{2}}\right)\left[\mathrm{2cos}\:\left(\frac{\frac{{A}\:−{B}}{\mathrm{2}}\:+\:\frac{{A}\:+{B}}{\mathrm{2}}}{\mathrm{2}}\right)\:\mathrm{cos}\left(\frac{\frac{{A}−{B}}{\mathrm{2}}−\frac{{A}\:+{B}}{\mathrm{2}}}{\mathrm{2}}\right)\right] \\ $$$$\:\:\:\:\:=\:\mathrm{2}\:\mathrm{cos}\:\left(\frac{{C}}{\mathrm{2}}\right)\left[\mathrm{2cos}\left(\frac{{A}}{\mathrm{2}}\right)\mathrm{cos}\:\left(−\frac{{B}}{\mathrm{2}}\right)\right] \\ $$$$\:\:\:\:\:=\:\mathrm{4}\:\mathrm{cos}\:\left(\frac{{A}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{B}}{\mathrm{2}}\right)\:\mathrm{cos}\:\left(\frac{{C}}{\mathrm{2}}\right)\:\mathrm{since}\:\mathrm{cos}\:{x}\:\mathrm{is}\:\mathrm{an}\:\mathrm{even}\:\mathrm{function}.\:{QED} \\ $$
Answered by 1549442205 last updated on 02/Jul/20
sinA+sinB=2sin((A+B)/2)cos((A−B)/2)=2cos(C/2)cos((A−B)/2) sinC=2sin(C/2)cos(C/2)=2cos(C/2)cos((A+B)/2).Hence, sinA+sinB+sinC=2cos(C/2)(cos((A−B)/2)+cos((A+B)/2)) =2cos(C/2).2cos((((A−B)/2)+((A+B)/2))/2)cos((((A−B)/2)−((A+B)/2))/2) =4cos(C/2)cos(A/2)cos((−B)/2)=4cos(A/2)cos(B/2)cos(C/2) (q.e.d)
$$\boldsymbol{\mathrm{sinA}}+\boldsymbol{\mathrm{sinB}}=\mathrm{2}\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\mathrm{A}}+\boldsymbol{\mathrm{B}}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{A}}−\boldsymbol{\mathrm{B}}}{\mathrm{2}}=\mathrm{2}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{C}}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{A}}−\boldsymbol{\mathrm{B}}}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{sinC}}=\mathrm{2}\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\mathrm{C}}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{C}}}{\mathrm{2}}=\mathrm{2}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{C}}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{A}}+\boldsymbol{\mathrm{B}}}{\mathrm{2}}.\boldsymbol{\mathrm{Hence}}, \\ $$$$\mathrm{s}\boldsymbol{\mathrm{inA}}+\boldsymbol{\mathrm{sinB}}+\boldsymbol{\mathrm{si}}\mathrm{n}\boldsymbol{\mathrm{C}}=\mathrm{2}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{C}}}{\mathrm{2}}\left(\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{A}}−\boldsymbol{\mathrm{B}}}{\mathrm{2}}+\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{A}}+\boldsymbol{\mathrm{B}}}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{C}}}{\mathrm{2}}.\mathrm{2}\boldsymbol{\mathrm{cos}}\frac{\frac{\boldsymbol{\mathrm{A}}−\boldsymbol{\mathrm{B}}}{\mathrm{2}}+\frac{\boldsymbol{\mathrm{A}}+\boldsymbol{\mathrm{B}}}{\mathrm{2}}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}\frac{\frac{\boldsymbol{\mathrm{A}}−\boldsymbol{\mathrm{B}}}{\mathrm{2}}−\frac{\boldsymbol{\mathrm{A}}+\boldsymbol{\mathrm{B}}}{\mathrm{2}}}{\mathrm{2}} \\ $$$$=\mathrm{4}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{C}}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{A}}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}\frac{−\boldsymbol{\mathrm{B}}}{\mathrm{2}}=\mathrm{4}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{A}}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{B}}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{C}}}{\mathrm{2}} \\ $$$$\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *