Question Number 101471 by I want to learn more last updated on 02/Jul/20
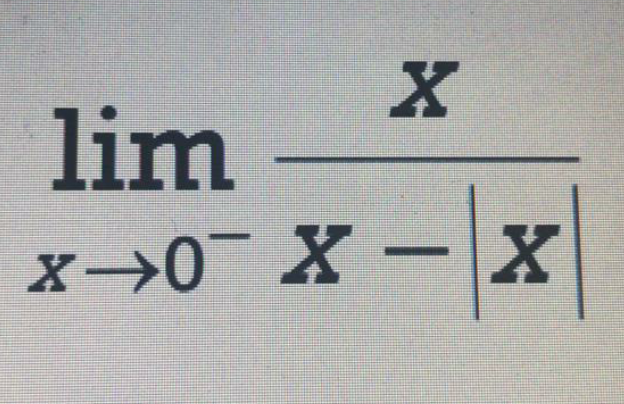
Commented by mr W last updated on 02/Jul/20
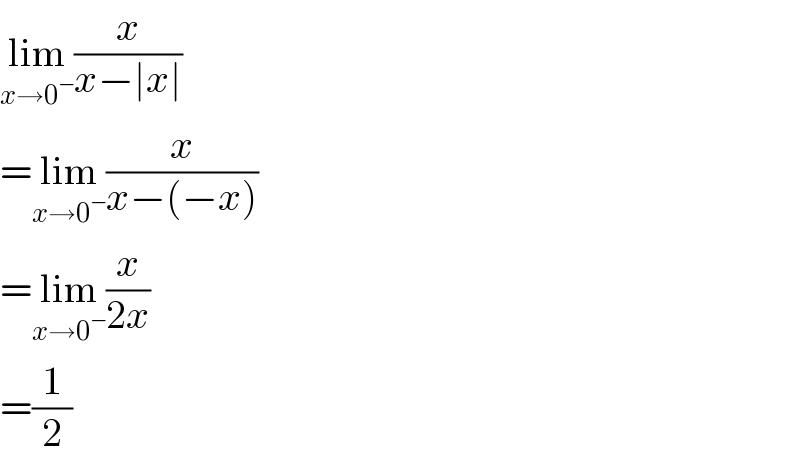
$$\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\frac{{x}}{{x}−\mid{x}\mid} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\frac{{x}}{{x}−\left(−{x}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\frac{{x}}{\mathrm{2}{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by I want to learn more last updated on 02/Jul/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Commented by bemath last updated on 03/Jul/20
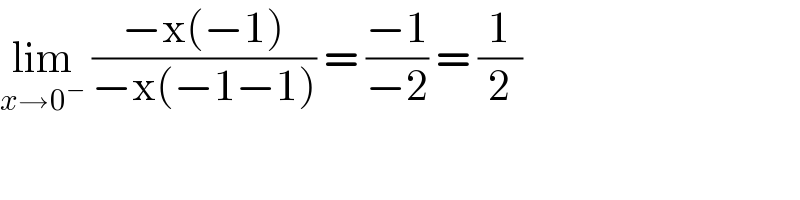
$$\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\frac{−\mathrm{x}\left(−\mathrm{1}\right)}{−\mathrm{x}\left(−\mathrm{1}−\mathrm{1}\right)}\:=\:\frac{−\mathrm{1}}{−\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by I want to learn more last updated on 03/Jul/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
