Question-101489

Question Number 101489 by bramlex last updated on 03/Jul/20

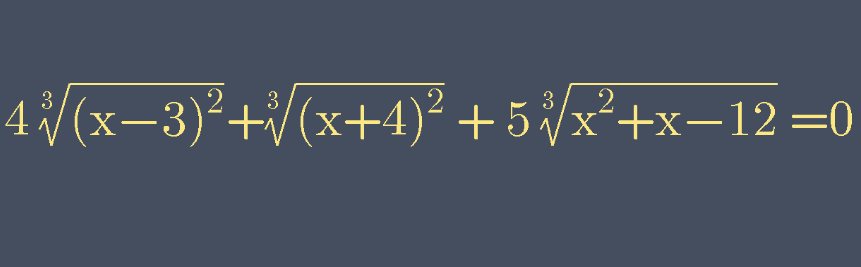
Answered by john santu last updated on 03/Jul/20

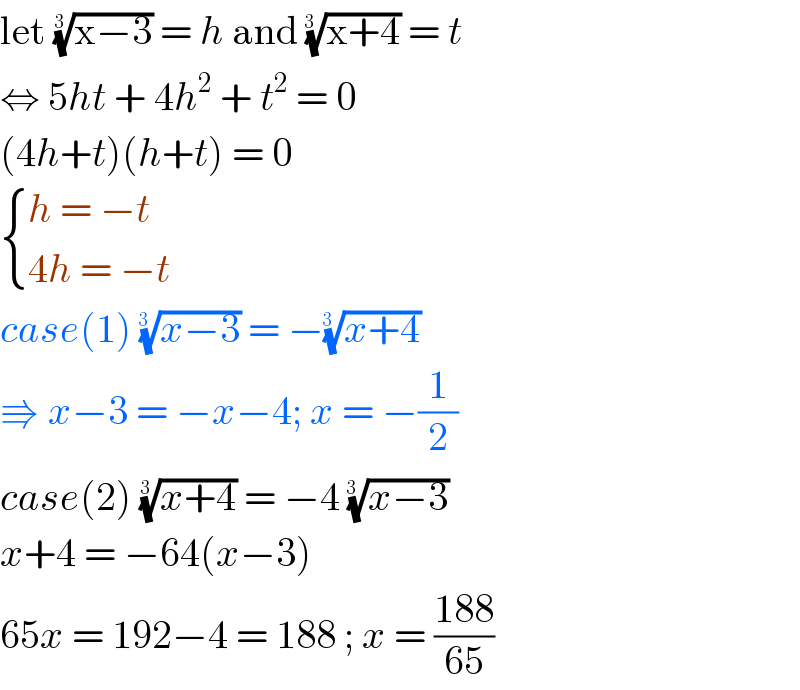
let ((x−3))^(1/(3 )) = h and ((x+4))^(1/(3 )) = t ⇔ 5ht + 4h^2 + t^2 = 0 (4h+t)(h+t) = 0 { ((h = −t)),((4h = −t)) :} case(1) ((x−3))^(1/(3 )) = −((x+4))^(1/(3 )) ⇛ x−3 = −x−4; x = −(1/2) case(2) ((x+4))^(1/(3 )) = −4 ((x−3))^(1/(3 )) x+4 = −64(x−3) 65x = 192−4 = 188 ; x = ((188)/(65))

$$\mathrm{let}\:\sqrt[{\mathrm{3}\:}]{\mathrm{x}−\mathrm{3}}\:=\:{h}\:\mathrm{and}\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{x}+\mathrm{4}}\:=\:{t} \\ $$$$\Leftrightarrow\:\mathrm{5}{ht}\:+\:\mathrm{4}{h}^{\mathrm{2}} \:+\:{t}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\left(\mathrm{4}{h}+{t}\right)\left({h}+{t}\right)\:=\:\mathrm{0} \\ $$$$\begin{cases}{{h}\:=\:−{t}}\\{\mathrm{4}{h}\:=\:−{t}}\end{cases} \\ $$$${case}\left(\mathrm{1}\right)\:\sqrt[{\mathrm{3}\:\:}]{{x}−\mathrm{3}}\:=\:−\sqrt[{\mathrm{3}\:\:}]{{x}+\mathrm{4}} \\ $$$$\Rrightarrow\:{x}−\mathrm{3}\:=\:−{x}−\mathrm{4};\:{x}\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${case}\left(\mathrm{2}\right)\:\sqrt[{\mathrm{3}\:}]{{x}+\mathrm{4}}\:=\:−\mathrm{4}\:\sqrt[{\mathrm{3}\:\:}]{{x}−\mathrm{3}} \\ $$$${x}+\mathrm{4}\:=\:−\mathrm{64}\left({x}−\mathrm{3}\right) \\ $$$$\mathrm{65}{x}\:=\:\mathrm{192}−\mathrm{4}\:=\:\mathrm{188}\:;\:{x}\:=\:\frac{\mathrm{188}}{\mathrm{65}}\: \\ $$

Facebook Tweet Pin

Question-101489

Leave a Reply Cancel reply