Question-101491

Question Number 101491 by bobhans last updated on 03/Jul/20

Commented by bemath last updated on 03/Jul/20

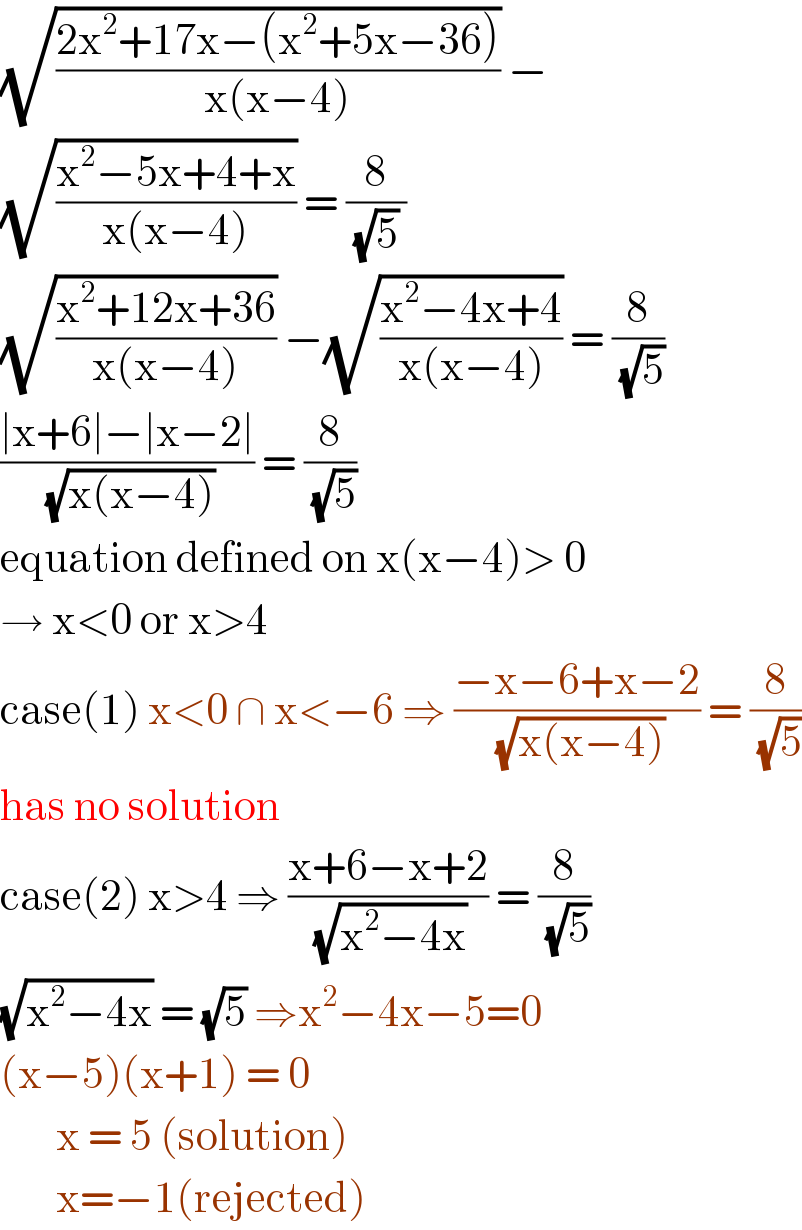
(√((2x^2 +17x−(x^2 +5x−36))/(x(x−4)))) − (√((x^2 −5x+4+x)/(x(x−4)))) = (8/( (√5) )) (√((x^2 +12x+36)/(x(x−4)))) −(√((x^2 −4x+4)/(x(x−4)))) = (8/( (√5))) ((∣x+6∣−∣x−2∣)/( (√(x(x−4))))) = (8/( (√5))) equation defined on x(x−4)> 0 → x<0 or x>4 case(1) x<0 ∩ x<−6 ⇒ ((−x−6+x−2)/( (√(x(x−4))))) = (8/( (√5))) has no solution case(2) x>4 ⇒ ((x+6−x+2)/( (√(x^2 −4x)))) = (8/( (√5))) (√(x^2 −4x)) = (√5) ⇒x^2 −4x−5=0 (x−5)(x+1) = 0 x = 5 (solution) x=−1(rejected)

$$\sqrt{\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{17x}−\left(\mathrm{x}^{\mathrm{2}} +\mathrm{5x}−\mathrm{36}\right)}{\mathrm{x}\left(\mathrm{x}−\mathrm{4}\right)}}\:− \\ $$$$\sqrt{\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{4}+\mathrm{x}}{\mathrm{x}\left(\mathrm{x}−\mathrm{4}\right)}}\:=\:\frac{\mathrm{8}}{\:\sqrt{\mathrm{5}}\:} \\ $$$$\sqrt{\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{12x}+\mathrm{36}}{\mathrm{x}\left(\mathrm{x}−\mathrm{4}\right)}}\:−\sqrt{\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{4}}{\mathrm{x}\left(\mathrm{x}−\mathrm{4}\right)}}\:=\:\frac{\mathrm{8}}{\:\sqrt{\mathrm{5}}} \\ $$$$\frac{\mid\mathrm{x}+\mathrm{6}\mid−\mid\mathrm{x}−\mathrm{2}\mid}{\:\sqrt{\mathrm{x}\left(\mathrm{x}−\mathrm{4}\right)}}\:=\:\frac{\mathrm{8}}{\:\sqrt{\mathrm{5}}}\: \\ $$$$\mathrm{equation}\:\mathrm{defined}\:\mathrm{on}\:\mathrm{x}\left(\mathrm{x}−\mathrm{4}\right)>\:\mathrm{0} \\ $$$$\rightarrow\:\mathrm{x}<\mathrm{0}\:\mathrm{or}\:\mathrm{x}>\mathrm{4} \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\:\mathrm{x}<\mathrm{0}\:\cap\:\mathrm{x}<−\mathrm{6}\:\Rightarrow\:\frac{−\mathrm{x}−\mathrm{6}+\mathrm{x}−\mathrm{2}}{\:\sqrt{\mathrm{x}\left(\mathrm{x}−\mathrm{4}\right)}}\:=\:\frac{\mathrm{8}}{\:\sqrt{\mathrm{5}}} \\ $$$$\mathrm{has}\:\mathrm{no}\:\mathrm{solution} \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\:\mathrm{x}>\mathrm{4}\:\Rightarrow\:\frac{\mathrm{x}+\mathrm{6}−\mathrm{x}+\mathrm{2}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}}}\:=\:\frac{\mathrm{8}}{\:\sqrt{\mathrm{5}}} \\ $$$$\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}}\:=\:\sqrt{\mathrm{5}}\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{4x}−\mathrm{5}=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{5}\right)\left(\mathrm{x}+\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{x}\:=\:\mathrm{5}\:\left(\mathrm{solution}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{x}=−\mathrm{1}\left(\mathrm{rejected}\right)\: \\ $$

Commented by bobhans last updated on 03/Jul/20

$$\mathrm{how}\:\mathrm{sir}?? \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply