Menu Close

Question-101563

Tinku Tara 0 Comments
Pin




Question Number 101563 by harckinwunmy last updated on 03/Jul/20
Answered by bramlex last updated on 03/Jul/20
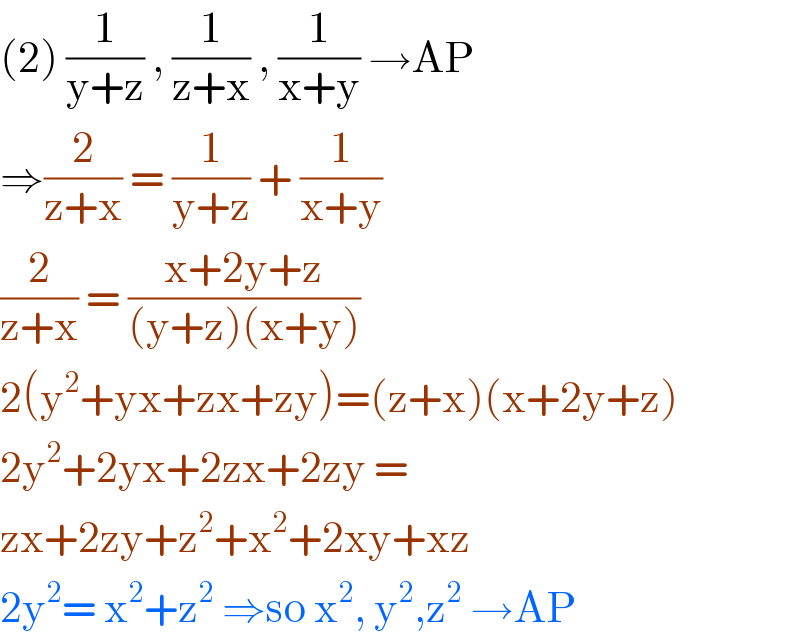
(2) (1/(y+z)) , (1/(z+x)) , (1/(x+y)) →AP ⇒(2/(z+x)) = (1/(y+z)) + (1/(x+y)) (2/(z+x)) = ((x+2y+z)/((y+z)(x+y))) 2(y^2 +yx+zx+zy)=(z+x)(x+2y+z) 2y^2 +2yx+2zx+2zy = zx+2zy+z^2 +x^2 +2xy+xz 2y^2 = x^2 +z^2 ⇒so x^2 , y^2 ,z^2 →AP
$$\left(\mathrm{2}\right)\:\frac{\mathrm{1}}{\mathrm{y}+\mathrm{z}}\:,\:\frac{\mathrm{1}}{\mathrm{z}+\mathrm{x}}\:,\:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{y}}\:\rightarrow\mathrm{AP} \\ $$$$\Rightarrow\frac{\mathrm{2}}{\mathrm{z}+\mathrm{x}}\:=\:\frac{\mathrm{1}}{\mathrm{y}+\mathrm{z}}\:+\:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{y}} \\ $$$$\frac{\mathrm{2}}{\mathrm{z}+\mathrm{x}}\:=\:\frac{\mathrm{x}+\mathrm{2y}+\mathrm{z}}{\left(\mathrm{y}+\mathrm{z}\right)\left(\mathrm{x}+\mathrm{y}\right)} \\ $$$$\mathrm{2}\left(\mathrm{y}^{\mathrm{2}} +\mathrm{yx}+\mathrm{zx}+\mathrm{zy}\right)=\left(\mathrm{z}+\mathrm{x}\right)\left(\mathrm{x}+\mathrm{2y}+\mathrm{z}\right) \\ $$$$\mathrm{2y}^{\mathrm{2}} +\mathrm{2yx}+\mathrm{2zx}+\mathrm{2zy}\:= \\ $$$$\mathrm{zx}+\mathrm{2zy}+\mathrm{z}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{xz} \\ $$$$\mathrm{2y}^{\mathrm{2}} =\:\mathrm{x}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \:\Rightarrow\mathrm{so}\:\mathrm{x}^{\mathrm{2}} ,\:\mathrm{y}^{\mathrm{2}} ,\mathrm{z}^{\mathrm{2}} \:\rightarrow\mathrm{AP} \\ $$
Answered by PRITHWISH SEN 2 last updated on 03/Jul/20
∵ a,b and c are the three cosecutive terms of a linear sequence ∴ a+c=2b now a((1/b)+(1/c))+c((1/a)+(1/b)) =((b(a^2 +c^2 )+ac(a+c))/(abc)) =((b(a^2 +c^2 )+2abc)/(abc)) =(((a+c)^2 )/(ac)) = ((2b(a+c))/(ac)) =2b((1/a)+(1/c)) ∴ the terms are also the 3 consecutive terms of the same linear sequence proved
$$\because\:\mathrm{a},\mathrm{b}\:\mathrm{and}\:\mathrm{c}\:\mathrm{are}\:\mathrm{the}\:\mathrm{three}\:\mathrm{cosecutive}\:\mathrm{terms}\:\mathrm{of} \\ $$$$\mathrm{a}\:\boldsymbol{\mathrm{linear}}\:\boldsymbol{\mathrm{sequence}} \\ $$$$\therefore\:\mathrm{a}+\mathrm{c}=\mathrm{2b} \\ $$$$\mathrm{now}\:\mathrm{a}\left(\frac{\mathrm{1}}{\mathrm{b}}+\frac{\mathrm{1}}{\mathrm{c}}\right)+\mathrm{c}\left(\frac{\mathrm{1}}{\mathrm{a}}+\frac{\mathrm{1}}{\mathrm{b}}\right) \\ $$$$=\frac{\mathrm{b}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)+\mathrm{ac}\left(\mathrm{a}+\mathrm{c}\right)}{\mathrm{abc}} \\ $$$$=\frac{\mathrm{b}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)+\mathrm{2abc}}{\mathrm{abc}}\:=\frac{\left(\mathrm{a}+\mathrm{c}\right)^{\mathrm{2}} }{\mathrm{ac}}\:=\:\frac{\mathrm{2b}\left(\mathrm{a}+\mathrm{c}\right)}{\mathrm{ac}} \\ $$$$=\mathrm{2b}\left(\frac{\mathrm{1}}{\mathrm{a}}+\frac{\mathrm{1}}{\mathrm{c}}\right) \\ $$$$\therefore\:\mathrm{the}\:\mathrm{terms}\:\mathrm{are}\:\mathrm{also}\:\mathrm{the}\:\mathrm{3}\:\mathrm{consecutive}\:\mathrm{terms}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{same}\:\mathrm{linear}\:\mathrm{sequence}\:\:\boldsymbol{\mathrm{proved}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *