Question Number 101610 by bramlex last updated on 03/Jul/20

Answered by john santu last updated on 04/Jul/20
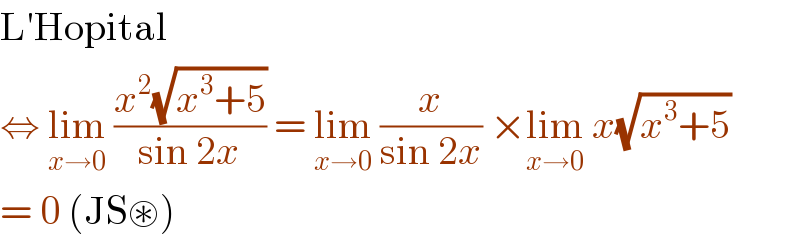
$$\mathrm{L}'\mathrm{Hopital} \\ $$$$\Leftrightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{3}} +\mathrm{5}}}{\mathrm{sin}\:\mathrm{2}{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}}{\mathrm{sin}\:\mathrm{2}{x}}\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}\sqrt{{x}^{\mathrm{3}} +\mathrm{5}} \\ $$$$=\:\mathrm{0}\:\left(\mathrm{JS}\circledast\right) \\ $$
Answered by Dwaipayan Shikari last updated on 04/Jul/20
![lim_(x→0) (((1/3)∫_0 ^x 2u^2 du)/(sin^2 x))=lim_(x→0) (((2/9)[u^3 ]_(√5) ^(√(x^3 +5)) )/(sin^2 x))=lim_(x→0) (((2/9)[(x^3 +5)^(2/3) −5^(2/3) ])/(x^2 sin^2 x)).x^2 lim_(x→0) (((2/9)[(x^3 +5)^(2/3) −5^(2/3) ])/((x^3 +5)−5)).((x^2 x)/x^2 )=(2/9).(2/3) 5^(1/3) .x= 0 (DS) ■★{assuming sinx=x}](https://www.tinkutara.com/question/Q101613.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{{x}} \mathrm{2}{u}^{\mathrm{2}} {du}}{{sin}^{\mathrm{2}} {x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{2}}{\mathrm{9}}\left[{u}^{\mathrm{3}} \right]_{\sqrt{\mathrm{5}}} ^{\sqrt{{x}^{\mathrm{3}} +\mathrm{5}}} }{{sin}^{\mathrm{2}} {x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{2}}{\mathrm{9}}\left[\left({x}^{\mathrm{3}} +\mathrm{5}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{5}^{\frac{\mathrm{2}}{\mathrm{3}}} \right]}{{x}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}}.{x}^{\mathrm{2}} \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{2}}{\mathrm{9}}\left[\left({x}^{\mathrm{3}} +\mathrm{5}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{5}^{\frac{\mathrm{2}}{\mathrm{3}}} \right]}{\left({x}^{\mathrm{3}} +\mathrm{5}\right)−\mathrm{5}}.\frac{{x}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{9}}.\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{3}}} .{x}=\:\:\:\mathrm{0}\:\:\left({DS}\right)\:\:\blacksquare\bigstar\left\{\mathrm{assuming}\:\mathrm{sinx}=\mathrm{x}\right\} \\ $$$$ \\ $$
