Question Number 101615 by john santu last updated on 03/Jul/20
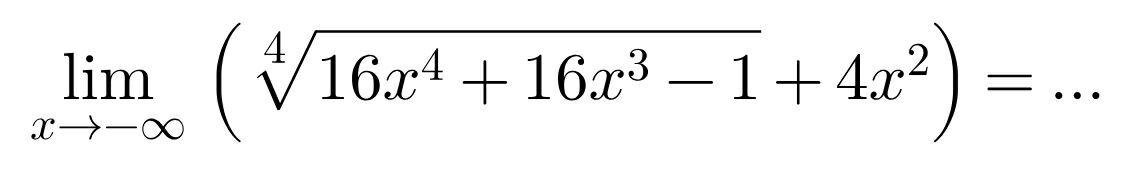
Commented by bramlex last updated on 03/Jul/20

$$\mathrm{i}\:\mathrm{got}\:−\infty\:\mathrm{sir}\: \\ $$
Commented by john santu last updated on 04/Jul/20
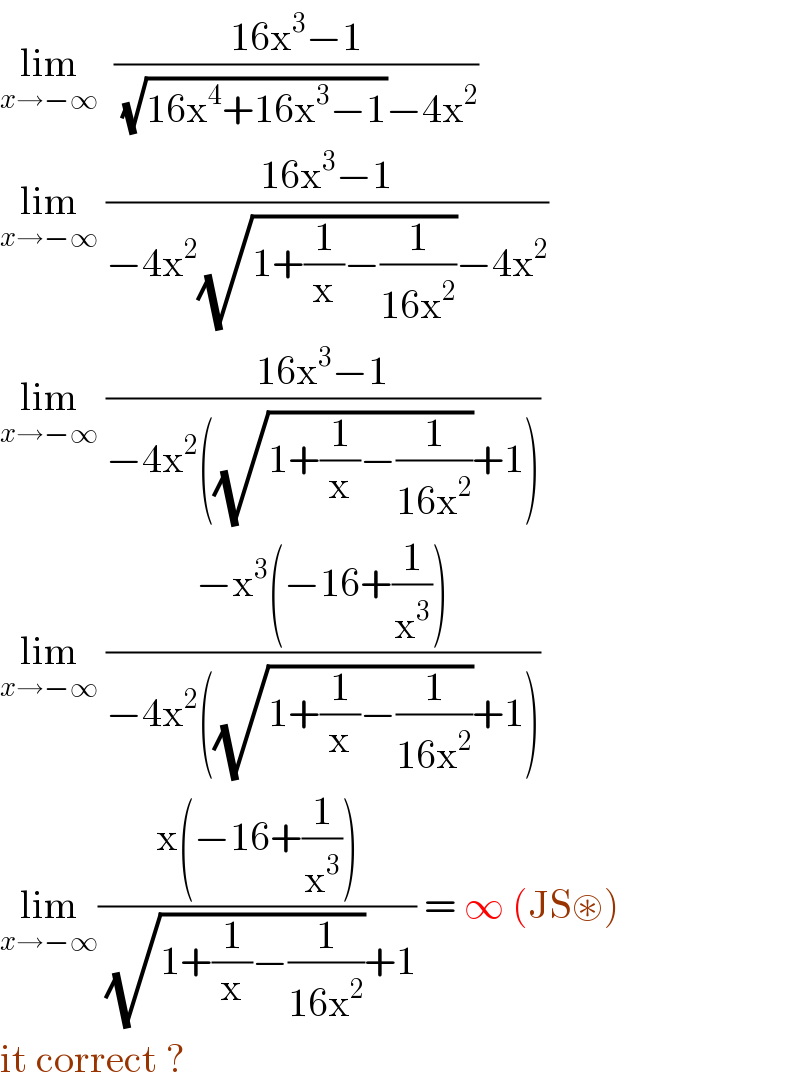
$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\:\frac{\mathrm{16x}^{\mathrm{3}} −\mathrm{1}}{\:\sqrt{\mathrm{16x}^{\mathrm{4}} +\mathrm{16x}^{\mathrm{3}} −\mathrm{1}}−\mathrm{4x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{16x}^{\mathrm{3}} −\mathrm{1}}{−\mathrm{4x}^{\mathrm{2}} \sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{16x}^{\mathrm{2}} }}−\mathrm{4x}^{\mathrm{2}} }\: \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{16x}^{\mathrm{3}} −\mathrm{1}}{−\mathrm{4x}^{\mathrm{2}} \left(\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{16x}^{\mathrm{2}} }}+\mathrm{1}\right)} \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{−\mathrm{x}^{\mathrm{3}} \left(−\mathrm{16}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)}{−\mathrm{4x}^{\mathrm{2}} \left(\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{16x}^{\mathrm{2}} }}+\mathrm{1}\right)} \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\mathrm{x}\left(−\mathrm{16}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{16x}^{\mathrm{2}} }}+\mathrm{1}}\:=\:\infty\:\left(\mathrm{JS}\circledast\right) \\ $$$$\mathrm{it}\:\mathrm{correct}\:? \\ $$
Commented by john santu last updated on 04/Jul/20
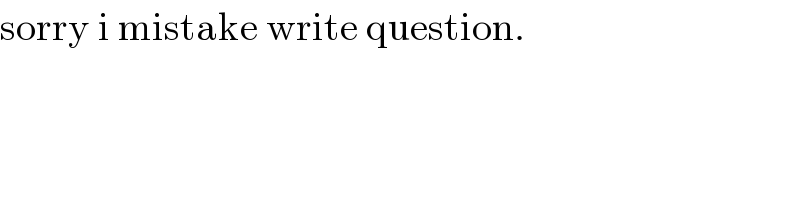
$$\mathrm{sorry}\:\mathrm{i}\:\mathrm{mistake}\:\mathrm{write}\:\mathrm{question}.\: \\ $$
Commented by john santu last updated on 04/Jul/20
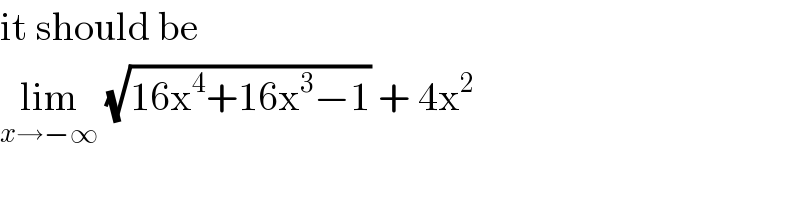
$$\mathrm{it}\:\mathrm{should}\:\mathrm{be}\: \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\sqrt{\mathrm{16x}^{\mathrm{4}} +\mathrm{16x}^{\mathrm{3}} −\mathrm{1}}\:+\:\mathrm{4x}^{\mathrm{2}} \: \\ $$
Answered by bramlex last updated on 04/Jul/20
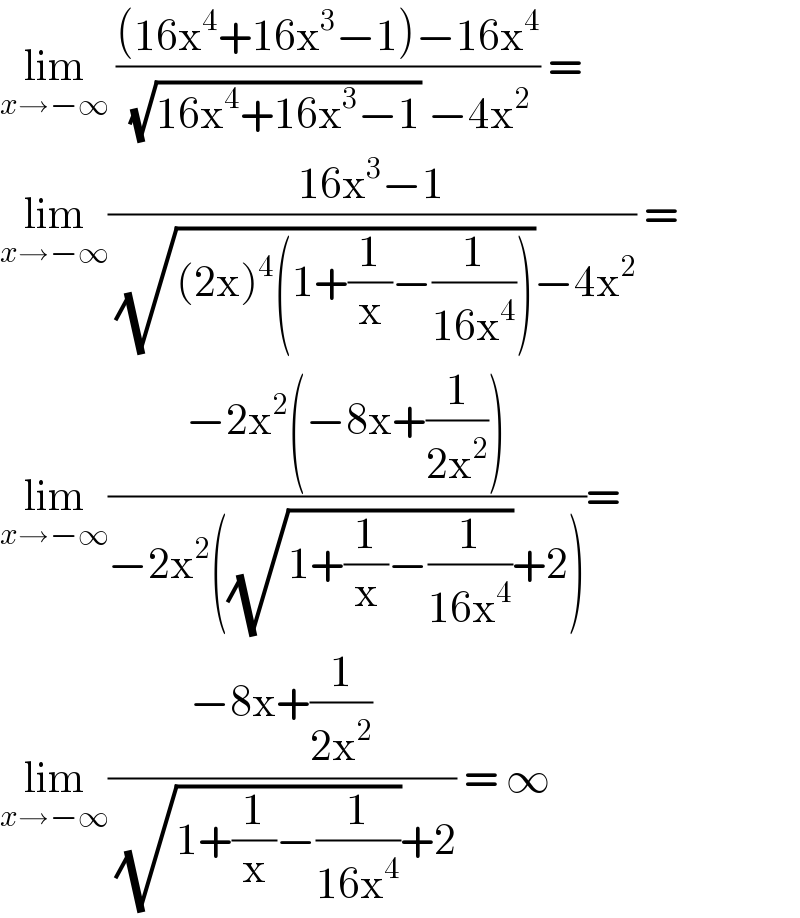
$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\left(\mathrm{16x}^{\mathrm{4}} +\mathrm{16x}^{\mathrm{3}} −\mathrm{1}\right)−\mathrm{16x}^{\mathrm{4}} }{\:\sqrt[{\:}]{\mathrm{16x}^{\mathrm{4}} +\mathrm{16x}^{\mathrm{3}} −\mathrm{1}}\:−\mathrm{4x}^{\mathrm{2}} }\:= \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\mathrm{16x}^{\mathrm{3}} −\mathrm{1}}{\:\sqrt{\left(\mathrm{2x}\right)^{\mathrm{4}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{16x}^{\mathrm{4}} }\right)}−\mathrm{4x}^{\mathrm{2}} }\:= \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{−\mathrm{2x}^{\mathrm{2}} \left(−\mathrm{8x}+\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} }\right)}{−\mathrm{2x}^{\mathrm{2}} \left(\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{16x}^{\mathrm{4}} }}+\mathrm{2}\right)}= \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{−\mathrm{8x}+\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{16x}^{\mathrm{4}} }}+\mathrm{2}}\:=\:\infty \\ $$
Commented by bramlex last updated on 03/Jul/20

$$\mathrm{oo}\:\mathrm{sorry}\:\mathrm{sir}.\:\mathrm{you}\:\mathrm{are}\:\mathrm{right} \\ $$
Answered by Dwaipayan Shikari last updated on 04/Jul/20
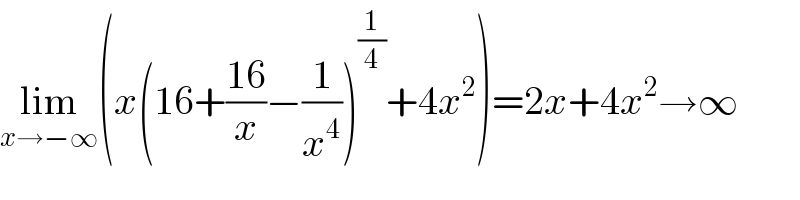
$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left({x}\left(\mathrm{16}+\frac{\mathrm{16}}{{x}}−\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right)^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{4}{x}^{\mathrm{2}} \right)=\mathrm{2}{x}+\mathrm{4}{x}^{\mathrm{2}} \rightarrow\infty \\ $$
Answered by mathmax by abdo last updated on 05/Jul/20
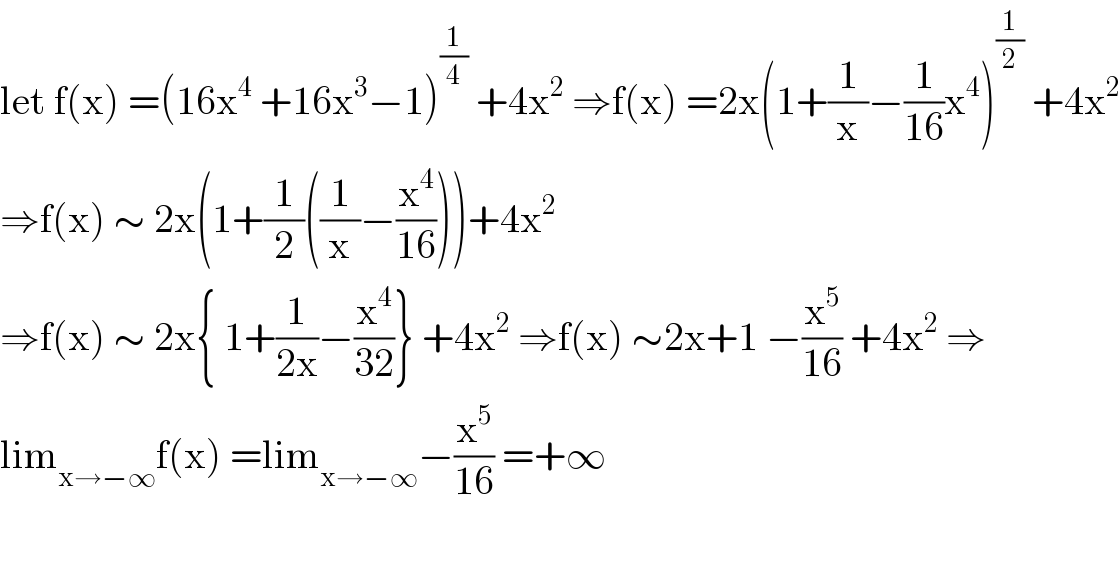
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\left(\mathrm{16x}^{\mathrm{4}} \:+\mathrm{16x}^{\mathrm{3}} −\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:+\mathrm{4x}^{\mathrm{2}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{2x}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{16}}\mathrm{x}^{\mathrm{4}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:+\mathrm{4x}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:\sim\:\mathrm{2x}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{16}}\right)\right)+\mathrm{4x}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:\sim\:\mathrm{2x}\left\{\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2x}}−\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{32}}\right\}\:+\mathrm{4x}^{\mathrm{2}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:\sim\mathrm{2x}+\mathrm{1}\:−\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{16}}\:+\mathrm{4x}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} −\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{16}}\:=+\infty \\ $$$$ \\ $$
