Question Number 101686 by bemath last updated on 04/Jul/20

Commented by bemath last updated on 05/Jul/20
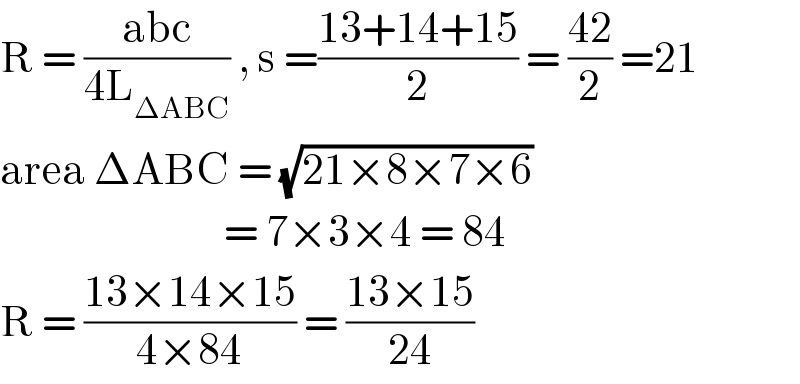
$$\mathrm{R}\:=\:\frac{\mathrm{abc}}{\mathrm{4L}_{\Delta\mathrm{ABC}} }\:,\:\mathrm{s}\:=\frac{\mathrm{13}+\mathrm{14}+\mathrm{15}}{\mathrm{2}}\:=\:\frac{\mathrm{42}}{\mathrm{2}}\:=\mathrm{21} \\ $$$$\mathrm{area}\:\Delta\mathrm{ABC}\:=\:\sqrt{\mathrm{21}×\mathrm{8}×\mathrm{7}×\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{7}×\mathrm{3}×\mathrm{4}\:=\:\mathrm{84} \\ $$$$\mathrm{R}\:=\:\frac{\mathrm{13}×\mathrm{14}×\mathrm{15}}{\mathrm{4}×\mathrm{84}}\:=\:\frac{\mathrm{13}×\mathrm{15}}{\mathrm{24}} \\ $$
Commented by bobhans last updated on 04/Jul/20
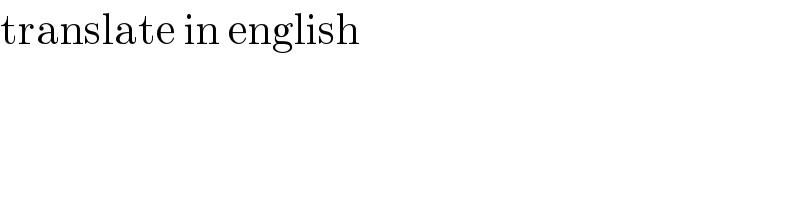
$$\mathrm{translate}\:\mathrm{in}\:\mathrm{english}\: \\ $$
Commented by bemath last updated on 04/Jul/20
In the figure the outer circle of the triangle abc is drawn if AB = 13, BC = 14 and AC = 15. Find the shortest distance from the center of the circle to AB
Commented by bobhans last updated on 04/Jul/20
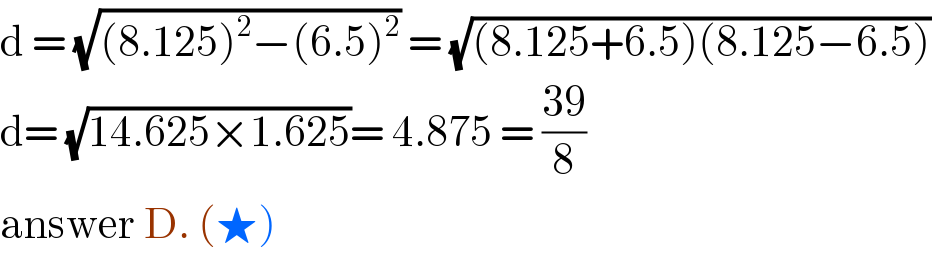
$$\mathrm{d}\:=\:\sqrt{\left(\mathrm{8}.\mathrm{125}\right)^{\mathrm{2}} −\left(\mathrm{6}.\mathrm{5}\right)^{\mathrm{2}} }\:=\:\sqrt{\left(\mathrm{8}.\mathrm{125}+\mathrm{6}.\mathrm{5}\right)\left(\mathrm{8}.\mathrm{125}−\mathrm{6}.\mathrm{5}\right)} \\ $$$$\mathrm{d}=\:\sqrt{\mathrm{14}.\mathrm{625}×\mathrm{1}.\mathrm{625}}=\:\mathrm{4}.\mathrm{875}\:=\:\frac{\mathrm{39}}{\mathrm{8}} \\ $$$$\mathrm{answer}\:\mathrm{D}.\:\left(\bigstar\right) \\ $$
Commented by 1549442205 last updated on 05/Jul/20

$$\mathrm{By}\:\mathrm{above}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{the}\:\mathrm{question}\:\mathrm{mus}\:\mathrm{be} \\ $$$$''\mathrm{Find}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circumcircle}\:\mathrm{of}\: \\ $$$$\mathrm{the}\:\mathrm{triangle}\:\mathrm{ABC}''.\mathrm{R}=\frac{\mathrm{13}×\mathrm{15}}{\mathrm{24}} \\ $$$$\mathrm{d}=\sqrt{\mathrm{R}^{\mathrm{2}} −\left(\frac{\mathrm{AB}}{\mathrm{2}}\right)^{\mathrm{2}} }=\sqrt{\left(\frac{\mathrm{13}×\mathrm{15}}{\mathrm{24}}\right)^{\mathrm{2}} −\frac{\mathrm{13}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$=\sqrt{\frac{\mathrm{13}^{\mathrm{2}} }{\mathrm{4}}×\left(\frac{\mathrm{15}^{\mathrm{2}} }{\mathrm{12}^{\mathrm{2}} }−\mathrm{1}\right)}=\frac{\mathrm{13}}{\mathrm{2}}\sqrt{\frac{\mathrm{15}^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} }{\mathrm{12}^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{13}}{\mathrm{24}}\sqrt{\mathrm{81}}=\frac{\mathrm{39}}{\mathrm{8}} \\ $$
