Menu Close

Question-101800

Tinku Tara 0 Comments
Pin




Question Number 101800 by Quvonchbek last updated on 04/Jul/20
Commented by mr W last updated on 05/Jul/20
very interesting! thanks sir!
$${very}\:{interesting}!\:{thanks}\:{sir}! \\ $$
Commented by mr W last updated on 04/Jul/20
what is the question?
$${what}\:{is}\:{the}\:{question}? \\ $$
Commented by prakash jain last updated on 05/Jul/20
http://ramanujan.sirinudi.org/Volumes/published/ram03.html Check above link for more theoritical description. in fact same equation is also covered answer that i added is same steps and some help from online simultaneous equation solvers
Answered by prakash jain last updated on 05/Jul/20
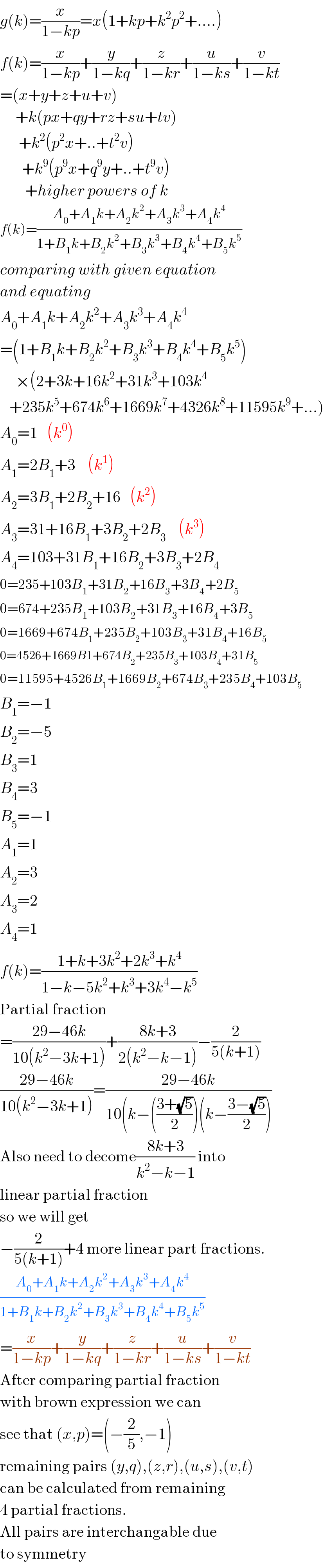
g(k)=(x/(1−kp))=x(1+kp+k^2 p^2 +....) f(k)=(x/(1−kp))+(y/(1−kq))+(z/(1−kr))+(u/(1−ks))+(v/(1−kt)) =(x+y+z+u+v) +k(px+qy+rz+su+tv) +k^2 (p^2 x+..+t^2 v) +k^9 (p^9 x+q^9 y+..+t^9 v) +higher powers of k f(k)=((A_0 +A_1 k+A_2 k^2 +A_3 k^3 +A_4 k^4 )/(1+B_1 k+B_2 k^2 +B_3 k^3 +B_4 k^4 +B_5 k^5 )) comparing with given equation and equating A_0 +A_1 k+A_2 k^2 +A_3 k^3 +A_4 k^4 =(1+B_1 k+B_2 k^2 +B_3 k^3 +B_4 k^4 +B_5 k^5 ) ×(2+3k+16k^2 +31k^3 +103k^4 +235k^5 +674k^6 +1669k^7 +4326k^8 +11595k^9 +...) A_0 =1 (k^0 ) A_1 =2B_1 +3 (k^1 ) A_2 =3B_1 +2B_2 +16 (k^2 ) A_3 =31+16B_1 +3B_2 +2B_3 (k^3 ) A_4 =103+31B_1 +16B_2 +3B_3 +2B_4 0=235+103B_1 +31B_2 +16B_3 +3B_4 +2B_5 0=674+235B_1 +103B_2 +31B_3 +16B_4 +3B_5 0=1669+674B_1 +235B_2 +103B_3 +31B_4 +16B_5 0=4526+1669B1+674B_2 +235B_3 +103B_4 +31B_5 0=11595+4526B_1 +1669B_2 +674B_3 +235B_4 +103B_5 B_1 =−1 B_2 =−5 B_3 =1 B_4 =3 B_5 =−1 A_1 =1 A_2 =3 A_3 =2 A_4 =1 f(k)=((1+k+3k^2 +2k^3 +k^4 )/(1−k−5k^2 +k^3 +3k^4 −k^5 )) Partial fraction =((29−46k)/(10(k^2 −3k+1)))+((8k+3)/(2(k^2 −k−1)))−(2/(5(k+1))) ((29−46k)/(10(k^2 −3k+1)))=((29−46k)/(10(k−(((3+(√5))/2))(k−((3−(√5))/2)))) Also need to decome((8k+3)/(k^2 −k−1)) into linear partial fraction so we will get −(2/(5(k+1)))+4 more linear part fractions. ((A_0 +A_1 k+A_2 k^2 +A_3 k^3 +A_4 k^4 )/(1+B_1 k+B_2 k^2 +B_3 k^3 +B_4 k^4 +B_5 k^5 )) =(x/(1−kp))+(y/(1−kq))+(z/(1−kr))+(u/(1−ks))+(v/(1−kt)) After comparing partial fraction with brown expression we can see that (x,p)=(−(2/5),−1) remaining pairs (y,q),(z,r),(u,s),(v,t) can be calculated from remaining 4 partial fractions. All pairs are interchangable due to symmetry
$${g}\left({k}\right)=\frac{{x}}{\mathrm{1}−{kp}}={x}\left(\mathrm{1}+{kp}+{k}^{\mathrm{2}} {p}^{\mathrm{2}} +….\right) \\ $$$${f}\left({k}\right)=\frac{{x}}{\mathrm{1}−{kp}}+\frac{{y}}{\mathrm{1}−{kq}}+\frac{{z}}{\mathrm{1}−{kr}}+\frac{{u}}{\mathrm{1}−{ks}}+\frac{{v}}{\mathrm{1}−{kt}} \\ $$$$=\left({x}+{y}+{z}+{u}+{v}\right) \\ $$$$\:\:\:\:\:+{k}\left({px}+{qy}+{rz}+{su}+{tv}\right) \\ $$$$\:\:\:\:\:\:+{k}^{\mathrm{2}} \left({p}^{\mathrm{2}} {x}+..+{t}^{\mathrm{2}} {v}\right) \\ $$$$\:\:\:\:\:\:\:+{k}^{\mathrm{9}} \left({p}^{\mathrm{9}} {x}+{q}^{\mathrm{9}} {y}+..+{t}^{\mathrm{9}} {v}\right) \\ $$$$\:\:\:\:\:\:\:\:+{higher}\:{powers}\:{of}\:{k} \\ $$$${f}\left({k}\right)=\frac{{A}_{\mathrm{0}} +{A}_{\mathrm{1}} {k}+{A}_{\mathrm{2}} {k}^{\mathrm{2}} +{A}_{\mathrm{3}} {k}^{\mathrm{3}} +{A}_{\mathrm{4}} {k}^{\mathrm{4}} }{\mathrm{1}+{B}_{\mathrm{1}} {k}+{B}_{\mathrm{2}} {k}^{\mathrm{2}} +{B}_{\mathrm{3}} {k}^{\mathrm{3}} +{B}_{\mathrm{4}} {k}^{\mathrm{4}} +{B}_{\mathrm{5}} {k}^{\mathrm{5}} } \\ $$$${comparing}\:{with}\:{given}\:{equation} \\ $$$${and}\:{equating} \\ $$$${A}_{\mathrm{0}} +{A}_{\mathrm{1}} {k}+{A}_{\mathrm{2}} {k}^{\mathrm{2}} +{A}_{\mathrm{3}} {k}^{\mathrm{3}} +{A}_{\mathrm{4}} {k}^{\mathrm{4}} \\ $$$$=\left(\mathrm{1}+{B}_{\mathrm{1}} {k}+{B}_{\mathrm{2}} {k}^{\mathrm{2}} +{B}_{\mathrm{3}} {k}^{\mathrm{3}} +{B}_{\mathrm{4}} {k}^{\mathrm{4}} +{B}_{\mathrm{5}} {k}^{\mathrm{5}} \right) \\ $$$$\:\:\:\:\:×\left(\mathrm{2}+\mathrm{3}{k}+\mathrm{16}{k}^{\mathrm{2}} +\mathrm{31}{k}^{\mathrm{3}} +\mathrm{103}{k}^{\mathrm{4}} \right. \\ $$$$\left.\:\:\:+\mathrm{235}{k}^{\mathrm{5}} +\mathrm{674}{k}^{\mathrm{6}} +\mathrm{1669}{k}^{\mathrm{7}} +\mathrm{4326}{k}^{\mathrm{8}} +\mathrm{11595}{k}^{\mathrm{9}} +…\right) \\ $$$${A}_{\mathrm{0}} =\mathrm{1}\:\:\:\left({k}^{\mathrm{0}} \right) \\ $$$${A}_{\mathrm{1}} =\mathrm{2}{B}_{\mathrm{1}} +\mathrm{3}\:\:\:\:\left({k}^{\mathrm{1}} \right) \\ $$$${A}_{\mathrm{2}} =\mathrm{3}{B}_{\mathrm{1}} +\mathrm{2}{B}_{\mathrm{2}} +\mathrm{16}\:\:\:\left({k}^{\mathrm{2}} \right) \\ $$$${A}_{\mathrm{3}} =\mathrm{31}+\mathrm{16}{B}_{\mathrm{1}} +\mathrm{3}{B}_{\mathrm{2}} +\mathrm{2}{B}_{\mathrm{3}} \:\:\:\:\left({k}^{\mathrm{3}} \right) \\ $$$${A}_{\mathrm{4}} =\mathrm{103}+\mathrm{31}{B}_{\mathrm{1}} +\mathrm{16}{B}_{\mathrm{2}} +\mathrm{3}{B}_{\mathrm{3}} +\mathrm{2}{B}_{\mathrm{4}} \\ $$$$\mathrm{0}=\mathrm{235}+\mathrm{103}{B}_{\mathrm{1}} +\mathrm{31}{B}_{\mathrm{2}} +\mathrm{16}{B}_{\mathrm{3}} +\mathrm{3}{B}_{\mathrm{4}} +\mathrm{2}{B}_{\mathrm{5}} \\ $$$$\mathrm{0}=\mathrm{674}+\mathrm{235}{B}_{\mathrm{1}} +\mathrm{103}{B}_{\mathrm{2}} +\mathrm{31}{B}_{\mathrm{3}} +\mathrm{16}{B}_{\mathrm{4}} +\mathrm{3}{B}_{\mathrm{5}} \\ $$$$\mathrm{0}=\mathrm{1669}+\mathrm{674}{B}_{\mathrm{1}} +\mathrm{235}{B}_{\mathrm{2}} +\mathrm{103}{B}_{\mathrm{3}} +\mathrm{31}{B}_{\mathrm{4}} +\mathrm{16}{B}_{\mathrm{5}} \\ $$$$\mathrm{0}=\mathrm{4526}+\mathrm{1669}{B}\mathrm{1}+\mathrm{674}{B}_{\mathrm{2}} +\mathrm{235}{B}_{\mathrm{3}} +\mathrm{103}{B}_{\mathrm{4}} +\mathrm{31}{B}_{\mathrm{5}} \\ $$$$\mathrm{0}=\mathrm{11595}+\mathrm{4526}{B}_{\mathrm{1}} +\mathrm{1669}{B}_{\mathrm{2}} +\mathrm{674}{B}_{\mathrm{3}} +\mathrm{235}{B}_{\mathrm{4}} +\mathrm{103}{B}_{\mathrm{5}} \\ $$$${B}_{\mathrm{1}} =−\mathrm{1} \\ $$$${B}_{\mathrm{2}} =−\mathrm{5} \\ $$$${B}_{\mathrm{3}} =\mathrm{1} \\ $$$${B}_{\mathrm{4}} =\mathrm{3} \\ $$$${B}_{\mathrm{5}} =−\mathrm{1} \\ $$$${A}_{\mathrm{1}} =\mathrm{1} \\ $$$${A}_{\mathrm{2}} =\mathrm{3} \\ $$$${A}_{\mathrm{3}} =\mathrm{2} \\ $$$${A}_{\mathrm{4}} =\mathrm{1} \\ $$$${f}\left({k}\right)=\frac{\mathrm{1}+{k}+\mathrm{3}{k}^{\mathrm{2}} +\mathrm{2}{k}^{\mathrm{3}} +{k}^{\mathrm{4}} }{\mathrm{1}−{k}−\mathrm{5}{k}^{\mathrm{2}} +{k}^{\mathrm{3}} +\mathrm{3}{k}^{\mathrm{4}} −{k}^{\mathrm{5}} } \\ $$$$\mathrm{Partial}\:\mathrm{fraction} \\ $$$$=\frac{\mathrm{29}−\mathrm{46}{k}}{\mathrm{10}\left({k}^{\mathrm{2}} −\mathrm{3}{k}+\mathrm{1}\right)}+\frac{\mathrm{8}{k}+\mathrm{3}}{\mathrm{2}\left({k}^{\mathrm{2}} −{k}−\mathrm{1}\right)}−\frac{\mathrm{2}}{\mathrm{5}\left({k}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{29}−\mathrm{46}{k}}{\mathrm{10}\left({k}^{\mathrm{2}} −\mathrm{3}{k}+\mathrm{1}\right)}=\frac{\mathrm{29}−\mathrm{46}{k}}{\mathrm{10}\left({k}−\left(\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\left({k}−\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\right.} \\ $$$$\mathrm{Also}\:\mathrm{need}\:\mathrm{to}\:\mathrm{decome}\frac{\mathrm{8}{k}+\mathrm{3}}{{k}^{\mathrm{2}} −{k}−\mathrm{1}}\:\mathrm{into} \\ $$$$\mathrm{linear}\:\mathrm{partial}\:\mathrm{fraction} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{will}\:\mathrm{get} \\ $$$$−\frac{\mathrm{2}}{\mathrm{5}\left({k}+\mathrm{1}\right)}+\mathrm{4}\:\mathrm{more}\:\mathrm{linear}\:\mathrm{part}\:\mathrm{fractions}. \\ $$$$\frac{{A}_{\mathrm{0}} +{A}_{\mathrm{1}} {k}+{A}_{\mathrm{2}} {k}^{\mathrm{2}} +{A}_{\mathrm{3}} {k}^{\mathrm{3}} +{A}_{\mathrm{4}} {k}^{\mathrm{4}} }{\mathrm{1}+{B}_{\mathrm{1}} {k}+{B}_{\mathrm{2}} {k}^{\mathrm{2}} +{B}_{\mathrm{3}} {k}^{\mathrm{3}} +{B}_{\mathrm{4}} {k}^{\mathrm{4}} +{B}_{\mathrm{5}} {k}^{\mathrm{5}} } \\ $$$$=\frac{{x}}{\mathrm{1}−{kp}}+\frac{{y}}{\mathrm{1}−{kq}}+\frac{{z}}{\mathrm{1}−{kr}}+\frac{{u}}{\mathrm{1}−{ks}}+\frac{{v}}{\mathrm{1}−{kt}} \\ $$$$\mathrm{After}\:\mathrm{comparing}\:\mathrm{partial}\:\mathrm{fraction} \\ $$$$\mathrm{with}\:\mathrm{brown}\:\mathrm{expression}\:\mathrm{we}\:\mathrm{can} \\ $$$$\mathrm{see}\:\mathrm{that}\:\left({x},{p}\right)=\left(−\frac{\mathrm{2}}{\mathrm{5}},−\mathrm{1}\right) \\ $$$$\mathrm{remaining}\:\mathrm{pairs}\:\left({y},{q}\right),\left({z},{r}\right),\left({u},{s}\right),\left({v},{t}\right) \\ $$$$\mathrm{can}\:\mathrm{be}\:\mathrm{calculated}\:\mathrm{from}\:\mathrm{remaining} \\ $$$$\mathrm{4}\:\mathrm{partial}\:\mathrm{fractions}. \\ $$$$\mathrm{All}\:\mathrm{pairs}\:\mathrm{are}\:\mathrm{interchangable}\:\mathrm{due} \\ $$$$\mathrm{to}\:\mathrm{symmetry} \\ $$
Commented by mr W last updated on 05/Jul/20
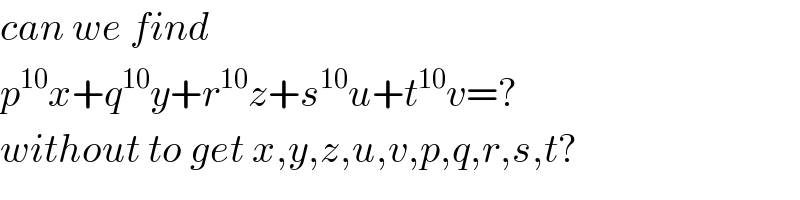
can we find p^(10) x+q^(10) y+r^(10) z+s^(10) u+t^(10) v=? without to get x,y,z,u,v,p,q,r,s,t?
$${can}\:{we}\:{find} \\ $$$${p}^{\mathrm{10}} {x}+{q}^{\mathrm{10}} {y}+{r}^{\mathrm{10}} {z}+{s}^{\mathrm{10}} {u}+{t}^{\mathrm{10}} {v}=? \\ $$$${without}\:{to}\:{get}\:{x},{y},{z},{u},{v},{p},{q},{r},{s},{t}? \\ $$
Commented by prakash jain last updated on 05/Jul/20
A_0 +A_1 k+A_2 k^2 +A_3 k^3 +A_4 k^4 =(1+B_1 k+B_2 k^2 +B_3 k^3 +B_4 k^4 )× (Σ_(i=0) ^9 a_i k^i +a_(10) k^(10) +...) a_0 to a_9 are given values. 0=a_(10) +B_1 a_9 +B_2 a_8 +B_3 a_7 +B_4 a_6 +B_5 a_5 a_(10) is unknown a_(10) −1∙11595−5∙4526+1∙1669+3∙674−1∙235=0 a_(10) =30769
$$ \\ $$$${A}_{\mathrm{0}} +{A}_{\mathrm{1}} {k}+{A}_{\mathrm{2}} {k}^{\mathrm{2}} +{A}_{\mathrm{3}} {k}^{\mathrm{3}} +{A}_{\mathrm{4}} {k}^{\mathrm{4}} \\ $$$$=\left(\mathrm{1}+{B}_{\mathrm{1}} {k}+{B}_{\mathrm{2}} {k}^{\mathrm{2}} +{B}_{\mathrm{3}} {k}^{\mathrm{3}} +{B}_{\mathrm{4}} {k}^{\mathrm{4}} \right)× \\ $$$$\left(\underset{{i}=\mathrm{0}} {\overset{\mathrm{9}} {\sum}}{a}_{{i}} {k}^{{i}} +{a}_{\mathrm{10}} {k}^{\mathrm{10}} +…\right) \\ $$$${a}_{\mathrm{0}} \:\mathrm{to}\:{a}_{\mathrm{9}} \:\mathrm{are}\:\mathrm{given}\:\mathrm{values}. \\ $$$$\mathrm{0}={a}_{\mathrm{10}} +{B}_{\mathrm{1}} {a}_{\mathrm{9}} +{B}_{\mathrm{2}} {a}_{\mathrm{8}} +{B}_{\mathrm{3}} {a}_{\mathrm{7}} +{B}_{\mathrm{4}} {a}_{\mathrm{6}} +{B}_{\mathrm{5}} {a}_{\mathrm{5}} \\ $$$${a}_{\mathrm{10}} \:\mathrm{is}\:\mathrm{unknown} \\ $$$${a}_{\mathrm{10}} −\mathrm{1}\centerdot\mathrm{11595}−\mathrm{5}\centerdot\mathrm{4526}+\mathrm{1}\centerdot\mathrm{1669}+\mathrm{3}\centerdot\mathrm{674}−\mathrm{1}\centerdot\mathrm{235}=\mathrm{0} \\ $$$${a}_{\mathrm{10}} =\mathrm{30769} \\ $$
Commented by prakash jain last updated on 05/Jul/20
Commented by prakash jain last updated on 05/Jul/20
For wolfram alpha calculation. I used answers given in paper.
$$\mathrm{For}\:\mathrm{wolfram}\:\mathrm{alpha}\:\mathrm{calculation}.\:\mathrm{I}\:\mathrm{used} \\ $$$$\mathrm{answers}\:\mathrm{given}\:\mathrm{in}\:\mathrm{paper}. \\ $$
Commented by mr W last updated on 05/Jul/20
very nice, thanks sir!
$${very}\:{nice},\:{thanks}\:{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *