Question-101974

Question Number 101974 by Ari last updated on 05/Jul/20

Commented by prakash jain last updated on 05/Jul/20

Can you please attach image to this question. There is an option to attach image

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{attach}\:\mathrm{image}\:\mathrm{to}\:\mathrm{this} \\ $$$$\mathrm{question}.\:\mathrm{There}\:\mathrm{is}\:\mathrm{an}\:\mathrm{option}\:\mathrm{to} \\ $$$$\mathrm{attach}\:\mathrm{image} \\ $$

Answered by Ari last updated on 05/Jul/20

Commented by prakash jain last updated on 06/Jul/20

Fig A ((πr^2 )/(πR^2 ))=(2/3)⇒(r^2 /R^2 )=(2/3) Fig C: Assume angle α for shaded area (((α/2)R^2 )/(πR^2 ))=(3/5)⇒α=((6π)/5) Fig B (shaded area angle (((α/2)r^2 )/(πR^2 ))=((((6π)/(10))r^2 )/(πR^2 ))=(6/(10))×(2/3)=(2/5)

$$\mathrm{Fig}\:\mathrm{A} \\ $$$$\frac{\pi{r}^{\mathrm{2}} }{\pi{R}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{3}}\Rightarrow\frac{{r}^{\mathrm{2}} }{{R}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{Fig}\:\mathrm{C}:\:\mathrm{Assume}\:\mathrm{angle}\:\alpha\:\mathrm{for}\:\mathrm{shaded}\:\mathrm{area} \\ $$$$\frac{\frac{\alpha}{\mathrm{2}}\mathrm{R}^{\mathrm{2}} }{\pi\mathrm{R}^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{5}}\Rightarrow\alpha=\frac{\mathrm{6}\pi}{\mathrm{5}} \\ $$$$\mathrm{Fig}\:\mathrm{B}\:\left({shaded}\:{area}\:{angle}\right. \\ $$$$\frac{\frac{\alpha}{\mathrm{2}}{r}^{\mathrm{2}} }{\pi{R}^{\mathrm{2}} }=\frac{\frac{\mathrm{6}\pi}{\mathrm{10}}{r}^{\mathrm{2}} }{\pi{R}^{\mathrm{2}} }=\frac{\mathrm{6}}{\mathrm{10}}×\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{2}}{\mathrm{5}} \\ $$

Commented by Ari last updated on 06/Jul/20

Yes,correct!

Answered by JDamian last updated on 06/Jul/20

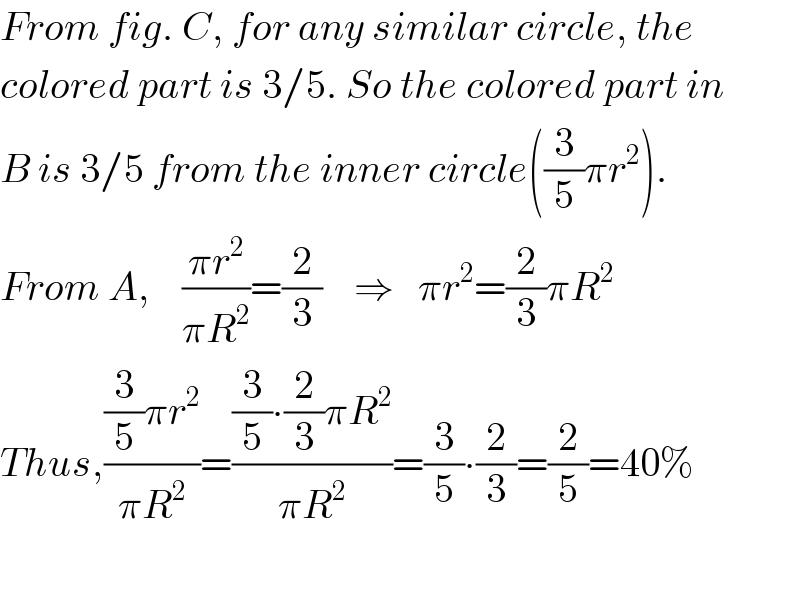
From fig. C, for any similar circle, the colored part is 3/5. So the colored part in B is 3/5 from the inner circle((3/5)πr^2 ). From A, ((πr^2 )/(πR^2 ))=(2/3) ⇒ πr^2 =(2/3)πR^2 Thus,(((3/5)πr^2 )/(πR^2 ))=(((3/5)∙(2/3)πR^2 )/(πR^2 ))=(3/5)∙(2/3)=(2/5)=40%

$${From}\:{fig}.\:{C},\:{for}\:{any}\:{similar}\:{circle},\:{the} \\ $$$${colored}\:{part}\:{is}\:\mathrm{3}/\mathrm{5}.\:{So}\:{the}\:{colored}\:{part}\:{in} \\ $$$${B}\:{is}\:\mathrm{3}/\mathrm{5}\:{from}\:{the}\:{inner}\:{circle}\left(\frac{\mathrm{3}}{\mathrm{5}}\pi{r}^{\mathrm{2}} \right). \\ $$$${From}\:{A},\:\:\:\:\frac{\pi{r}^{\mathrm{2}} }{\pi{R}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\:\Rightarrow\:\:\:\pi{r}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}\pi{R}^{\mathrm{2}} \\ $$$${Thus},\frac{\frac{\mathrm{3}}{\mathrm{5}}\pi{r}^{\mathrm{2}} }{\pi{R}^{\mathrm{2}} }=\frac{\frac{\mathrm{3}}{\mathrm{5}}\centerdot\frac{\mathrm{2}}{\mathrm{3}}\pi{R}^{\mathrm{2}} }{\pi{R}^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{5}}\centerdot\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{2}}{\mathrm{5}}=\mathrm{40\%} \\ $$$$ \\ $$

Commented by Ari last updated on 06/Jul/20

Yes,correct!

Facebook Tweet Pin

Leave a Reply Cancel reply