Question Number 102002 by Jamshidbek2311 last updated on 06/Jul/20
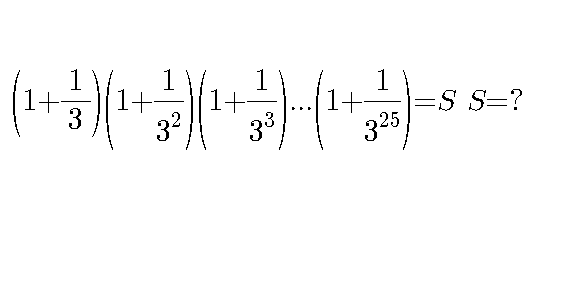
Commented by mr W last updated on 06/Jul/20
$${please}\:{don}'{t}\:{post}\:{the}\:{same}\:{question} \\ $$$${again}\:{and}\:{again}.\:{if}\:{you}\:{have}\:{doubt}, \\ $$$${give}\:{comment}\:{in}\:{the}\:{old}\:{thread},\:{don}'{t} \\ $$$${open}\:{a}\:{new}\:{thread}. \\ $$
Commented by mr W last updated on 06/Jul/20
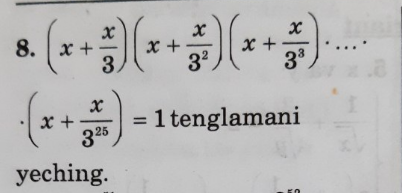
Commented by 1549442205 last updated on 06/Jul/20

$$\mathrm{I}\:\mathrm{guess}\:\mathrm{he}\left(\mathrm{she}\right)\:\mathrm{want}\:\mathrm{the}\:\mathrm{solvers}\:\mathrm{give}\:\mathrm{him} \\ $$$$\left(\mathrm{her}\right)\:\mathrm{a}\:\mathrm{particilar}\:\mathrm{result}\:\mathrm{with}\:\mathrm{true}\:\mathrm{number}\:\mathrm{which} \\ $$$$\mathrm{was}\:\mathrm{reduced} \\ $$
Commented by Jamshidbek2311 last updated on 06/Jul/20

$${ok}.{sorry} \\ $$
Commented by 06122004 last updated on 06/Jul/20
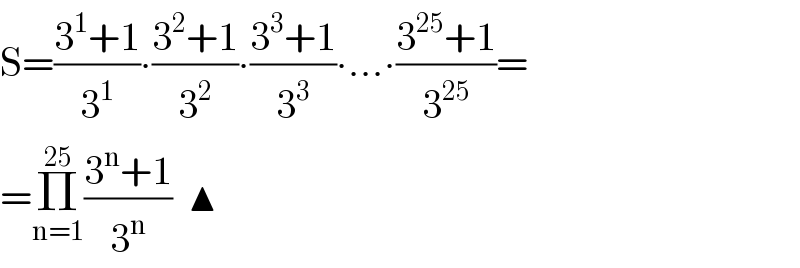
$$\mathrm{S}=\frac{\mathrm{3}^{\mathrm{1}} +\mathrm{1}}{\mathrm{3}^{\mathrm{1}} }\centerdot\frac{\mathrm{3}^{\mathrm{2}} +\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\centerdot\frac{\mathrm{3}^{\mathrm{3}} +\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }\centerdot…\centerdot\frac{\mathrm{3}^{\mathrm{25}} +\mathrm{1}}{\mathrm{3}^{\mathrm{25}} }= \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{25}} {\prod}}\frac{\mathrm{3}^{\mathrm{n}} +\mathrm{1}}{\mathrm{3}^{\mathrm{n}} }\:\:\blacktriangle \\ $$
Commented by prakash jain last updated on 06/Jul/20

$$\mathrm{Is}\:\mathrm{it}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{a}\:\mathrm{closed} \\ $$$$\mathrm{form}\:\mathrm{product}\:\mathrm{value}\:\mathrm{without} \\ $$$$\mathrm{actual}\:\mathrm{calculation}? \\ $$$$\mathrm{I}\:\mathrm{thought}\:\mathrm{about}\:\mathrm{it}\:\mathrm{for}\:\mathrm{a}\:\mathrm{long} \\ $$$$\mathrm{time}\:\mathrm{but}\:\mathrm{could}\:\mathrm{not}\:\mathrm{find}\:\mathrm{a}\:\mathrm{way}. \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{need}\:\mathrm{to}\:\mathrm{read}\:\mathrm{a}\:\mathrm{little}\:\mathrm{bit}\:\mathrm{more}. \\ $$
