Menu Close

Question-102078

Tinku Tara 0 Comments
Pin




Question Number 102078 by Jamshidbek2311 last updated on 06/Jul/20
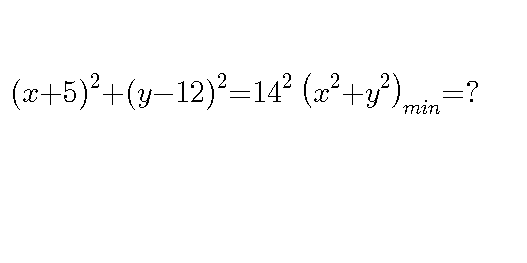
Answered by mr W last updated on 06/Jul/20
METHOD I x^2 +y^2 is the square of the distance from point (x,y) to the origin (0,0). (x+5)^2 +(y−12)^2 =14^2 is the circle with radius 14 and center at (−5,12). distance from (−5,12) to the origin is (√((−5)^2 +12^2 ))=13, the minimum distance from a point on the circle to the origin is then 14−13=1 and the maximum distance is 14+13=27. ⇒(x^2 +y^2 )_(min) =1^2 =1 ⇒(x^2 +y^2 )_(max) =27^2 =729
$$\boldsymbol{{METHOD}}\:\boldsymbol{{I}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:{is}\:{the}\:{square}\:{of}\:{the}\:{distance} \\ $$$${from}\:{point}\:\left({x},{y}\right)\:{to}\:{the}\:{origin}\:\left(\mathrm{0},\mathrm{0}\right). \\ $$$$ \\ $$$$\left({x}+\mathrm{5}\right)^{\mathrm{2}} +\left({y}−\mathrm{12}\right)^{\mathrm{2}} =\mathrm{14}^{\mathrm{2}} \:{is}\:{the}\:{circle} \\ $$$${with}\:{radius}\:\mathrm{14}\:{and}\:{center}\:{at}\:\left(−\mathrm{5},\mathrm{12}\right). \\ $$$${distance}\:{from}\:\left(−\mathrm{5},\mathrm{12}\right)\:{to}\:{the}\:{origin} \\ $$$${is}\:\sqrt{\left(−\mathrm{5}\right)^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} }=\mathrm{13},\:{the}\:{minimum} \\ $$$${distance}\:{from}\:{a}\:{point}\:{on}\:{the}\:{circle}\:{to} \\ $$$${the}\:{origin}\:{is}\:{then}\:\mathrm{14}−\mathrm{13}=\mathrm{1}\:{and}\:{the}\: \\ $$$${maximum}\:{distance}\:{is}\:\mathrm{14}+\mathrm{13}=\mathrm{27}. \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)_{{min}} =\mathrm{1}^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)_{{max}} =\mathrm{27}^{\mathrm{2}} =\mathrm{729} \\ $$
Answered by mr W last updated on 06/Jul/20
METHOD II k=x^2 +y^2 F=x^2 +y^2 +λ[(x+5)^2 +(y−12)^2 −14^2 ] (∂F/∂x)=2x+2λ(x+5)=0 ⇒x=−((5λ)/(λ+1)) (∂F/∂y)=2y+2λ(y−12)=0 ⇒y=((12λ)/(λ+1)) (−((5λ)/(λ+1))+5)^2 +(((12λ)/(λ+1))−12)^2 −14^2 =0 5^2 (1−(λ/(λ+1)))^2 +12^2 (1−(λ/(λ+1)))^2 −14^2 =0 13^2 (1−(λ/(λ+1)))^2 =14^2 ⇒1−(λ/(λ+1))=±((14)/(13)) ⇒λ+1=±((13)/(14)) ⇒λ=−(1/(14)) or −((27)/(14)) with λ=−(1/(14)): x=−5×((−(1/(14)))/(1−(1/(14))))=(5/(13)) y=12×((−(1/(14)))/(1−(1/(14))))=−((12)/(13)) ⇒k=x^2 +y^2 =((5/(13)))^2 +(−((12)/(13)))^2 =1=min. with λ=−((27)/(14)): x=−5×((−((27)/(14)))/(1−((27)/(14))))=−5×((27)/(13)) y=12×((−((27)/(14)))/(1−((27)/(14))))=12×((27)/(13)) ⇒k=x^2 +y^2 =(−5×((27)/(13)))^2 +(12×((27)/(13)))^2 =729=max.
$$\boldsymbol{{METHOD}}\:\boldsymbol{{II}} \\ $$$${k}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${F}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\lambda\left[\left({x}+\mathrm{5}\right)^{\mathrm{2}} +\left({y}−\mathrm{12}\right)^{\mathrm{2}} −\mathrm{14}^{\mathrm{2}} \right] \\ $$$$\frac{\partial{F}}{\partial{x}}=\mathrm{2}{x}+\mathrm{2}\lambda\left({x}+\mathrm{5}\right)=\mathrm{0}\:\Rightarrow{x}=−\frac{\mathrm{5}\lambda}{\lambda+\mathrm{1}} \\ $$$$\frac{\partial{F}}{\partial{y}}=\mathrm{2}{y}+\mathrm{2}\lambda\left({y}−\mathrm{12}\right)=\mathrm{0}\:\Rightarrow{y}=\frac{\mathrm{12}\lambda}{\lambda+\mathrm{1}} \\ $$$$\left(−\frac{\mathrm{5}\lambda}{\lambda+\mathrm{1}}+\mathrm{5}\right)^{\mathrm{2}} +\left(\frac{\mathrm{12}\lambda}{\lambda+\mathrm{1}}−\mathrm{12}\right)^{\mathrm{2}} −\mathrm{14}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{5}^{\mathrm{2}} \left(\mathrm{1}−\frac{\lambda}{\lambda+\mathrm{1}}\right)^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} \left(\mathrm{1}−\frac{\lambda}{\lambda+\mathrm{1}}\right)^{\mathrm{2}} −\mathrm{14}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{13}^{\mathrm{2}} \left(\mathrm{1}−\frac{\lambda}{\lambda+\mathrm{1}}\right)^{\mathrm{2}} =\mathrm{14}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{1}−\frac{\lambda}{\lambda+\mathrm{1}}=\pm\frac{\mathrm{14}}{\mathrm{13}} \\ $$$$\Rightarrow\lambda+\mathrm{1}=\pm\frac{\mathrm{13}}{\mathrm{14}} \\ $$$$\Rightarrow\lambda=−\frac{\mathrm{1}}{\mathrm{14}}\:{or}\:−\frac{\mathrm{27}}{\mathrm{14}} \\ $$$${with}\:\lambda=−\frac{\mathrm{1}}{\mathrm{14}}: \\ $$$${x}=−\mathrm{5}×\frac{−\frac{\mathrm{1}}{\mathrm{14}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{14}}}=\frac{\mathrm{5}}{\mathrm{13}} \\ $$$${y}=\mathrm{12}×\frac{−\frac{\mathrm{1}}{\mathrm{14}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{14}}}=−\frac{\mathrm{12}}{\mathrm{13}} \\ $$$$\Rightarrow{k}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\left(\frac{\mathrm{5}}{\mathrm{13}}\right)^{\mathrm{2}} +\left(−\frac{\mathrm{12}}{\mathrm{13}}\right)^{\mathrm{2}} =\mathrm{1}={min}. \\ $$$${with}\:\lambda=−\frac{\mathrm{27}}{\mathrm{14}}: \\ $$$${x}=−\mathrm{5}×\frac{−\frac{\mathrm{27}}{\mathrm{14}}}{\mathrm{1}−\frac{\mathrm{27}}{\mathrm{14}}}=−\mathrm{5}×\frac{\mathrm{27}}{\mathrm{13}} \\ $$$${y}=\mathrm{12}×\frac{−\frac{\mathrm{27}}{\mathrm{14}}}{\mathrm{1}−\frac{\mathrm{27}}{\mathrm{14}}}=\mathrm{12}×\frac{\mathrm{27}}{\mathrm{13}} \\ $$$$\Rightarrow{k}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\left(−\mathrm{5}×\frac{\mathrm{27}}{\mathrm{13}}\right)^{\mathrm{2}} +\left(\mathrm{12}×\frac{\mathrm{27}}{\mathrm{13}}\right)^{\mathrm{2}} =\mathrm{729}={max}. \\ $$
Answered by mr W last updated on 06/Jul/20
METHOD III k=x^2 +y^2 =d^2 let x=d cos θ, y=d sin θ (d cos θ+5)^2 +(d sin θ−12)^2 =14^2 d^2 +2d(5 cos θ−12 sin θ)−27=0 d^2 +26d(sin α cos θ−cos α sin θ)−27=0 d^2 +26d sin (α−θ)−27=0 d=−13 sin (α−θ)+(√(169 sin^2 (α−θ)+27)) d_(max) =13+(√(169+27))=13+14=27 d_(min) =−13+(√(169+27))=−13+14=1 k=x^2 +y^2 =d^2 =27^2 =729=max. k=x^2 +y^2 =d^2 =1^2 =1=min.
$$\boldsymbol{{METHOD}}\:\boldsymbol{{III}} \\ $$$${k}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={d}^{\mathrm{2}} \\ $$$${let}\:{x}={d}\:\mathrm{cos}\:\theta,\:{y}={d}\:\mathrm{sin}\:\theta \\ $$$$\left({d}\:\mathrm{cos}\:\theta+\mathrm{5}\right)^{\mathrm{2}} +\left({d}\:\mathrm{sin}\:\theta−\mathrm{12}\right)^{\mathrm{2}} =\mathrm{14}^{\mathrm{2}} \\ $$$${d}^{\mathrm{2}} +\mathrm{2}{d}\left(\mathrm{5}\:\mathrm{cos}\:\theta−\mathrm{12}\:\mathrm{sin}\:\theta\right)−\mathrm{27}=\mathrm{0} \\ $$$${d}^{\mathrm{2}} +\mathrm{26}{d}\left(\mathrm{sin}\:\alpha\:\mathrm{cos}\:\theta−\mathrm{cos}\:\alpha\:\mathrm{sin}\:\theta\right)−\mathrm{27}=\mathrm{0} \\ $$$${d}^{\mathrm{2}} +\mathrm{26}{d}\:\mathrm{sin}\:\left(\alpha−\theta\right)−\mathrm{27}=\mathrm{0} \\ $$$${d}=−\mathrm{13}\:\mathrm{sin}\:\left(\alpha−\theta\right)+\sqrt{\mathrm{169}\:\mathrm{sin}^{\mathrm{2}} \:\left(\alpha−\theta\right)+\mathrm{27}} \\ $$$${d}_{{max}} =\mathrm{13}+\sqrt{\mathrm{169}+\mathrm{27}}=\mathrm{13}+\mathrm{14}=\mathrm{27} \\ $$$${d}_{{min}} =−\mathrm{13}+\sqrt{\mathrm{169}+\mathrm{27}}=−\mathrm{13}+\mathrm{14}=\mathrm{1} \\ $$$${k}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={d}^{\mathrm{2}} =\mathrm{27}^{\mathrm{2}} =\mathrm{729}={max}. \\ $$$${k}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={d}^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} =\mathrm{1}={min}. \\ $$
Answered by mr W last updated on 06/Jul/20
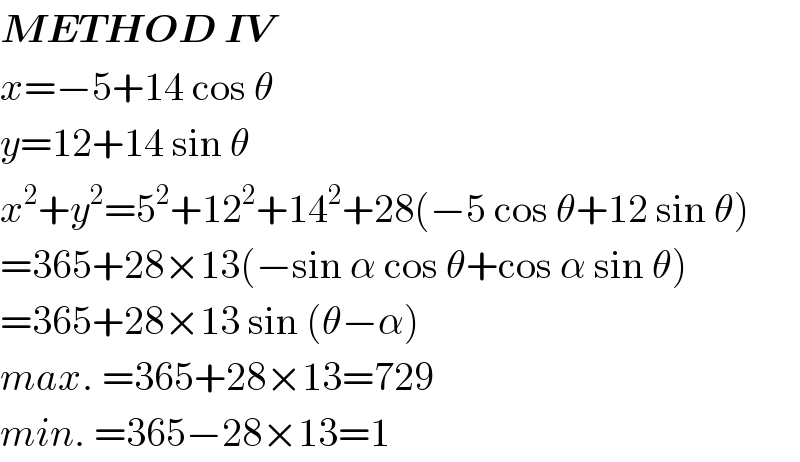
METHOD IV x=−5+14 cos θ y=12+14 sin θ x^2 +y^2 =5^2 +12^2 +14^2 +28(−5 cos θ+12 sin θ) =365+28×13(−sin α cos θ+cos α sin θ) =365+28×13 sin (θ−α) max. =365+28×13=729 min. =365−28×13=1
$$\boldsymbol{{METHOD}}\:\boldsymbol{{IV}} \\ $$$${x}=−\mathrm{5}+\mathrm{14}\:\mathrm{cos}\:\theta \\ $$$${y}=\mathrm{12}+\mathrm{14}\:\mathrm{sin}\:\theta \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} +\mathrm{14}^{\mathrm{2}} +\mathrm{28}\left(−\mathrm{5}\:\mathrm{cos}\:\theta+\mathrm{12}\:\mathrm{sin}\:\theta\right) \\ $$$$=\mathrm{365}+\mathrm{28}×\mathrm{13}\left(−\mathrm{sin}\:\alpha\:\mathrm{cos}\:\theta+\mathrm{cos}\:\alpha\:\mathrm{sin}\:\theta\right) \\ $$$$=\mathrm{365}+\mathrm{28}×\mathrm{13}\:\mathrm{sin}\:\left(\theta−\alpha\right) \\ $$$${max}.\:=\mathrm{365}+\mathrm{28}×\mathrm{13}=\mathrm{729} \\ $$$${min}.\:=\mathrm{365}−\mathrm{28}×\mathrm{13}=\mathrm{1} \\ $$
Answered by john santu last updated on 07/Jul/20
method JS x^2 +y_(min) ^2 = [ r −(√(x_c ^2 +y_c ^2 )) ]^2 x^2 +y_(max) ^2 = [ r +(√(x_c ^2 +y_c ^2 )) ]^2
$${method}\:{JS} \\ $$$${x}^{\mathrm{2}} +{y}_{{min}} ^{\mathrm{2}} \:=\:\left[\:{r}\:−\sqrt{{x}_{{c}} ^{\mathrm{2}} +{y}_{{c}} ^{\mathrm{2}} }\:\right]\:^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{y}_{{max}} ^{\mathrm{2}} \:=\:\left[\:{r}\:+\sqrt{{x}_{{c}} ^{\mathrm{2}} +{y}_{{c}} ^{\mathrm{2}} }\:\right]^{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *