Question-102177

Question Number 102177 by dw last updated on 07/Jul/20

Commented by Rasheed.Sindhi last updated on 07/Jul/20

ac+bd=0⇒d=−((ac)/b) c^2 +d^2 =c^2 +(−((ac)/b))^2 =1 ⇒b^2 c^2 +a^2 c^2 =b^2 c^2 (a^2 +b^2 )=b^2 c^2 =b^2 [∵ a^2 +b^2 =1] ⇒c=±b ⇒d=−((a(±b))/b)=∓a Now ab+cd=ab+(±b)(∓a) =ab−ab=0 ab+cd=0 ▲^⊚ _( ⌢)

$${ac}+{bd}=\mathrm{0}\Rightarrow{d}=−\frac{{ac}}{{b}} \\ $$$${c}^{\mathrm{2}} +{d}^{\mathrm{2}} ={c}^{\mathrm{2}} +\left(−\frac{{ac}}{{b}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{c}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)={b}^{\mathrm{2}} \:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{c}^{\mathrm{2}} ={b}^{\mathrm{2}} \:\:\:\:\:\:\left[\because\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{c}=\pm{b} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{d}=−\frac{{a}\left(\pm{b}\right)}{{b}}=\mp{a} \\ $$$${Now} \\ $$$${ab}+{cd}={ab}+\left(\pm{b}\right)\left(\mp{a}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:={ab}−{ab}=\mathrm{0} \\ $$$${ab}+{cd}=\mathrm{0}\:\underset{\:\:\:\:\frown} {\blacktriangle^{\circledcirc} }\: \\ $$

Commented by dw last updated on 07/Jul/20

$${Thak}\:{you}\:{sir}!\:{Good}\:{solution}. \\ $$

Answered by $@y@m last updated on 07/Jul/20

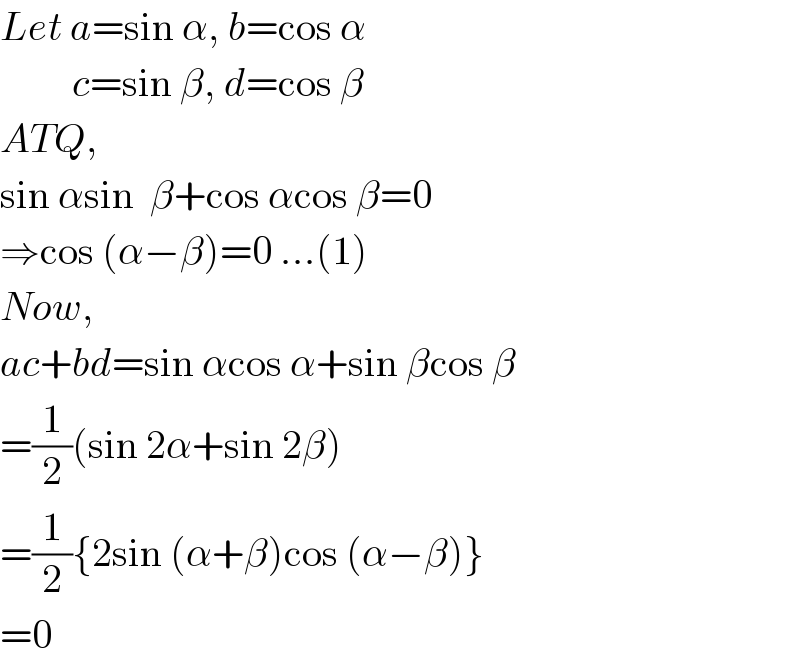
Let a=sin α, b=cos α c=sin β, d=cos β ATQ, sin αsin β+cos αcos β=0 ⇒cos (α−β)=0 ...(1) Now, ac+bd=sin αcos α+sin βcos β =(1/2)(sin 2α+sin 2β) =(1/2){2sin (α+β)cos (α−β)} =0

$${Let}\:{a}=\mathrm{sin}\:\alpha,\:{b}=\mathrm{cos}\:\alpha \\ $$$$\:\:\:\:\:\:\:\:\:{c}=\mathrm{sin}\:\beta,\:{d}=\mathrm{cos}\:\beta \\ $$$${ATQ}, \\ $$$$\mathrm{sin}\:\alpha\mathrm{sin}\:\:\beta+\mathrm{cos}\:\alpha\mathrm{cos}\:\beta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\left(\alpha−\beta\right)=\mathrm{0}\:…\left(\mathrm{1}\right) \\ $$$${Now}, \\ $$$${ac}+{bd}=\mathrm{sin}\:\alpha\mathrm{cos}\:\alpha+\mathrm{sin}\:\beta\mathrm{cos}\:\beta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}\:\mathrm{2}\alpha+\mathrm{sin}\:\mathrm{2}\beta\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{2sin}\:\left(\alpha+\beta\right)\mathrm{cos}\:\left(\alpha−\beta\right)\right\} \\ $$$$=\mathrm{0} \\ $$

Commented by dw last updated on 07/Jul/20

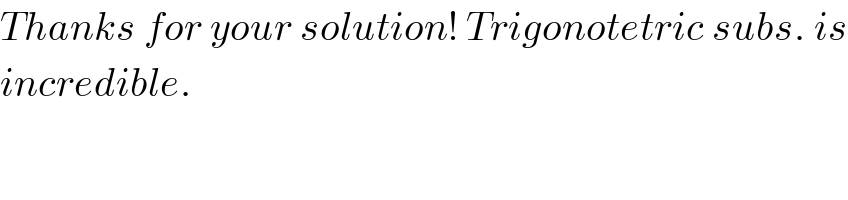
$${Thanks}\:{for}\:{your}\:{solution}!\:{Trigonotetric}\:{subs}.\:{is} \\ $$$${incredible}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply