Question Number 102313 by bemath last updated on 08/Jul/20

Answered by 1549442205 last updated on 08/Jul/20
![The abscissa of intersection point of the curve y=(4/( (√x)))−(4/x) and x−axis being the root of the eqs.(4/( (√x)))−(4/x)=0 ⇔x−(√x)=0(x≠0)⇔x=1.Hence, S=∫_0 ^1 e^(1−(1/4)x) dx+∫_1 ^4 [e^(1−(1/4)x) −((4/( (√x)))−(4/x))]dx ∫_0 ^4 e^(1−(1/4)x) dx+∫_1 ^4 (4/x)dx−∫_1 ^4 (4/( (√x)))dx =−4e^(1−(1/4)x) ∣_0 ^4 +4lnx∣_1 ^4 −8(√(x )) ∣_1 ^4 =−4−(−4e)+4(ln4−0)−8(2−1) =4e+8ln2−12](https://www.tinkutara.com/question/Q102321.png)
$$\mathrm{The}\:\mathrm{abscissa}\:\:\mathrm{of}\:\:\mathrm{intersection}\:\mathrm{point}\:\mathrm{of}\:\mathrm{the}\:\mathrm{curve}\: \\ $$$$\mathrm{y}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{x}}}−\frac{\mathrm{4}}{\mathrm{x}}\:\mathrm{and}\:\mathrm{x}−\mathrm{axis}\:\:\mathrm{being}\:\mathrm{the}\:\mathrm{root}\:\mathrm{of}\:\mathrm{the}\:\mathrm{eqs}.\frac{\mathrm{4}}{\:\sqrt{\mathrm{x}}}−\frac{\mathrm{4}}{\mathrm{x}}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}−\sqrt{\mathrm{x}}=\mathrm{0}\left(\mathrm{x}\neq\mathrm{0}\right)\Leftrightarrow\mathrm{x}=\mathrm{1}.\mathrm{Hence}, \\ $$$$\mathrm{S}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{e}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}} \mathrm{dx}+\int_{\mathrm{1}} ^{\mathrm{4}} \left[\mathrm{e}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}} −\left(\frac{\mathrm{4}}{\:\sqrt{\mathrm{x}}}−\frac{\mathrm{4}}{\mathrm{x}}\right)\right]\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{e}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}} \mathrm{dx}+\int_{\mathrm{1}} ^{\mathrm{4}} \frac{\mathrm{4}}{\mathrm{x}}\mathrm{dx}−\int_{\mathrm{1}} ^{\mathrm{4}} \frac{\mathrm{4}}{\:\sqrt{\mathrm{x}}}\mathrm{dx} \\ $$$$=−\mathrm{4e}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}} \mid_{\mathrm{0}} ^{\mathrm{4}} +\mathrm{4lnx}\mid_{\mathrm{1}} ^{\mathrm{4}} −\mathrm{8}\sqrt{\mathrm{x}\:}\:\overset{\mathrm{4}} {\mid}_{\mathrm{1}} \\ $$$$=−\mathrm{4}−\left(−\mathrm{4e}\right)+\mathrm{4}\left(\mathrm{ln4}−\mathrm{0}\right)−\mathrm{8}\left(\mathrm{2}−\mathrm{1}\right) \\ $$$$=\mathrm{4e}+\mathrm{8ln2}−\mathrm{12} \\ $$
Commented by I want to learn more last updated on 08/Jul/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by bemath last updated on 08/Jul/20
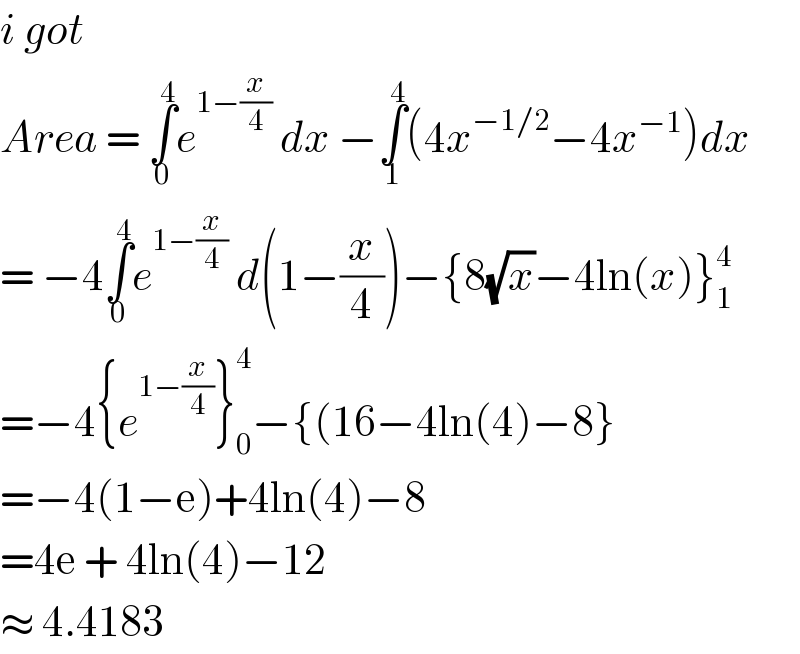
$${i}\:{got}\: \\ $$$${Area}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}{e}^{\mathrm{1}−\frac{{x}}{\mathrm{4}}} \:{dx}\:−\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\left(\mathrm{4}{x}^{−\mathrm{1}/\mathrm{2}} −\mathrm{4}{x}^{−\mathrm{1}} \right){dx} \\ $$$$=\:−\mathrm{4}\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}{e}^{\mathrm{1}−\frac{{x}}{\mathrm{4}}} \:{d}\left(\mathrm{1}−\frac{{x}}{\mathrm{4}}\right)−\left\{\mathrm{8}\sqrt{{x}}−\mathrm{4ln}\left({x}\right)\right\}_{\mathrm{1}} ^{\mathrm{4}} \\ $$$$=−\mathrm{4}\left\{{e}^{\mathrm{1}−\frac{{x}}{\mathrm{4}}} \right\}_{\mathrm{0}} ^{\mathrm{4}} −\left\{\left(\mathrm{16}−\mathrm{4ln}\left(\mathrm{4}\right)−\mathrm{8}\right\}\right. \\ $$$$=−\mathrm{4}\left(\mathrm{1}−\mathrm{e}\right)+\mathrm{4ln}\left(\mathrm{4}\right)−\mathrm{8} \\ $$$$=\mathrm{4e}\:+\:\mathrm{4ln}\left(\mathrm{4}\right)−\mathrm{12} \\ $$$$\approx\:\mathrm{4}.\mathrm{4183}\: \\ $$
Commented by I want to learn more last updated on 08/Jul/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
