Question Number 102328 by bemath last updated on 08/Jul/20
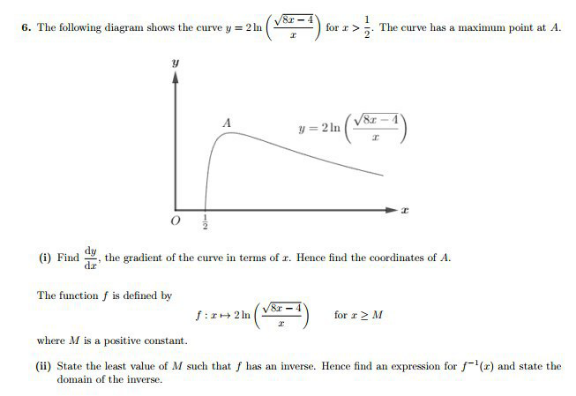
Answered by bobhans last updated on 08/Jul/20
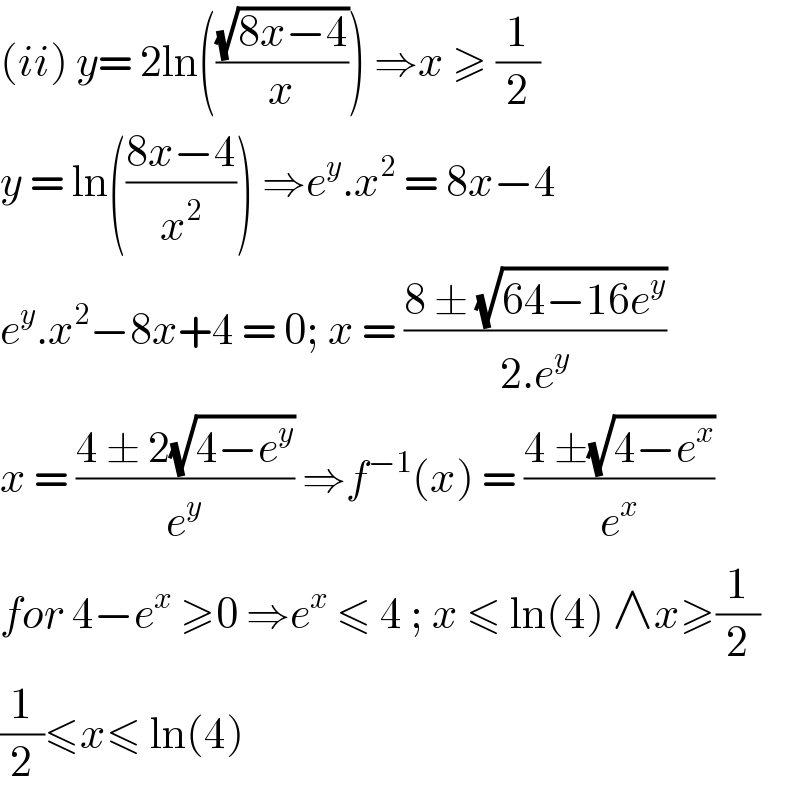
$$\left({ii}\right)\:{y}=\:\mathrm{2ln}\left(\frac{\sqrt{\mathrm{8}{x}−\mathrm{4}}}{{x}}\right)\:\Rightarrow{x}\:\geqslant\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}\:=\:\mathrm{ln}\left(\frac{\mathrm{8}{x}−\mathrm{4}}{{x}^{\mathrm{2}} }\right)\:\Rightarrow{e}^{{y}} .{x}^{\mathrm{2}} \:=\:\mathrm{8}{x}−\mathrm{4} \\ $$$${e}^{{y}} .{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{4}\:=\:\mathrm{0};\:{x}\:=\:\frac{\mathrm{8}\:\pm\:\sqrt{\mathrm{64}−\mathrm{16}{e}^{{y}} }}{\mathrm{2}.{e}^{{y}} } \\ $$$${x}\:=\:\frac{\mathrm{4}\:\pm\:\mathrm{2}\sqrt{\mathrm{4}−{e}^{{y}} }}{{e}^{{y}} }\:\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)\:=\:\frac{\mathrm{4}\:\pm\sqrt{\mathrm{4}−{e}^{{x}} }}{{e}^{{x}} } \\ $$$${for}\:\mathrm{4}−{e}^{{x}} \:\geqslant\mathrm{0}\:\Rightarrow{e}^{{x}} \:\leqslant\:\mathrm{4}\:;\:{x}\:\leqslant\:\mathrm{ln}\left(\mathrm{4}\right)\:\wedge{x}\geqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\leqslant{x}\leqslant\:\mathrm{ln}\left(\mathrm{4}\right) \\ $$
Commented by I want to learn more last updated on 08/Jul/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
