Question Number 102348 by mohammad17 last updated on 08/Jul/20

Answered by mr W last updated on 08/Jul/20
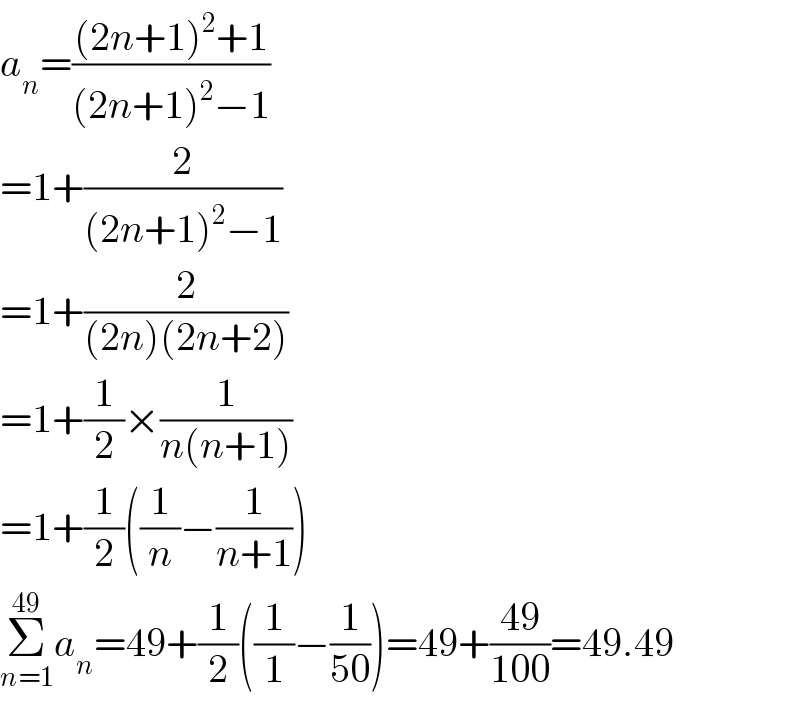
$${a}_{{n}} =\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\mathrm{1}+\frac{\mathrm{2}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\mathrm{1}+\frac{\mathrm{2}}{\left(\mathrm{2}{n}\right)\left(\mathrm{2}{n}+\mathrm{2}\right)} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{49}} {\sum}}{a}_{{n}} =\mathrm{49}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{50}}\right)=\mathrm{49}+\frac{\mathrm{49}}{\mathrm{100}}=\mathrm{49}.\mathrm{49} \\ $$
Commented by mohammad17 last updated on 08/Jul/20
$${nice}\:{sir}\:{thank}\:{you} \\ $$
