Question Number 102418 by Akeyz last updated on 09/Jul/20

Answered by Rasheed.Sindhi last updated on 09/Jul/20
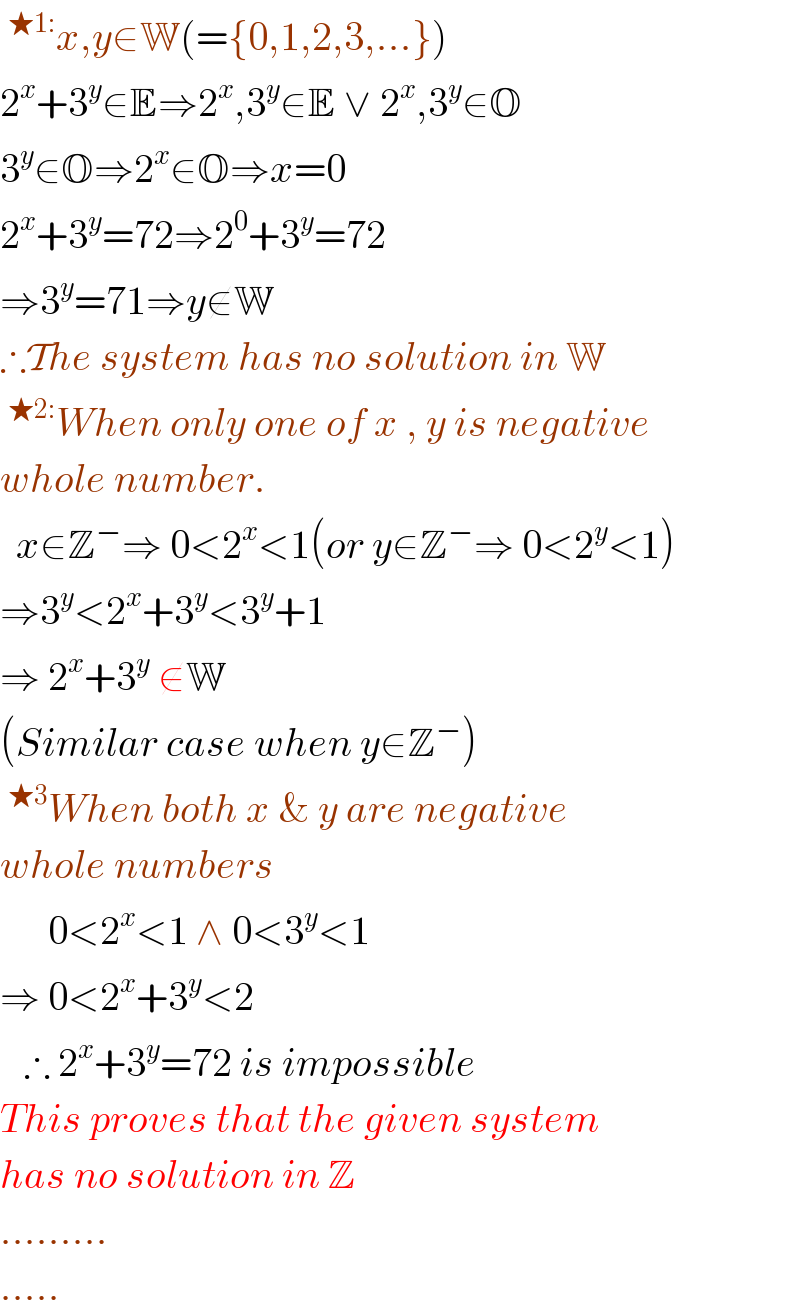
$$\:^{\bigstar\mathrm{1}:} {x},{y}\in\mathbb{W}\left(=\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},…\right\}\right) \\ $$$$\mathrm{2}^{{x}} +\mathrm{3}^{{y}} \in\mathbb{E}\Rightarrow\mathrm{2}^{{x}} ,\mathrm{3}^{{y}} \in\mathbb{E}\:\vee\:\mathrm{2}^{{x}} ,\mathrm{3}^{{y}} \in\mathbb{O} \\ $$$$\mathrm{3}^{{y}} \in\mathbb{O}\Rightarrow\mathrm{2}^{{x}} \in\mathbb{O}\Rightarrow{x}=\mathrm{0} \\ $$$$\mathrm{2}^{{x}} +\mathrm{3}^{{y}} =\mathrm{72}\Rightarrow\mathrm{2}^{\mathrm{0}} +\mathrm{3}^{{y}} =\mathrm{72} \\ $$$$\Rightarrow\mathrm{3}^{{y}} =\mathrm{71}\Rightarrow{y}\notin\mathbb{W} \\ $$$$\therefore\mathcal{T}{he}\:{system}\:{has}\:{no}\:{solution}\:{in}\:\mathbb{W}\: \\ $$$$\:^{\bigstar\mathrm{2}:} {When}\:{only}\:{one}\:{of}\:{x}\:,\:{y}\:{is}\:{negative} \\ $$$${whole}\:{number}. \\ $$$$\:\:{x}\in\mathbb{Z}^{−} \Rightarrow\:\mathrm{0}<\mathrm{2}^{{x}} <\mathrm{1}\left({or}\:{y}\in\mathbb{Z}^{−} \Rightarrow\:\mathrm{0}<\mathrm{2}^{{y}} <\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{3}^{{y}} <\mathrm{2}^{{x}} +\mathrm{3}^{{y}} <\mathrm{3}^{{y}} +\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{2}^{{x}} +\mathrm{3}^{{y}} \:\notin\mathbb{W} \\ $$$$\left({Similar}\:{case}\:{when}\:{y}\in\mathbb{Z}^{−} \right) \\ $$$$\:^{\bigstar\mathrm{3}} {When}\:{both}\:{x}\:\&\:{y}\:{are}\:{negative} \\ $$$${whole}\:{numbers} \\ $$$$\:\:\:\:\:\:\mathrm{0}<\mathrm{2}^{{x}} <\mathrm{1}\:\wedge\:\mathrm{0}<\mathrm{3}^{{y}} <\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{0}<\mathrm{2}^{{x}} +\mathrm{3}^{{y}} <\mathrm{2} \\ $$$$\:\:\:\therefore\:\mathrm{2}^{{x}} +\mathrm{3}^{{y}} =\mathrm{72}\:{is}\:{impossible} \\ $$$${This}\:{proves}\:{that}\:{the}\:{given}\:{system} \\ $$$${has}\:{no}\:{solution}\:{in}\:\mathbb{Z} \\ $$$$……… \\ $$$$….. \\ $$
