Question Number 102524 by ajfour last updated on 09/Jul/20

Commented by ajfour last updated on 09/Jul/20

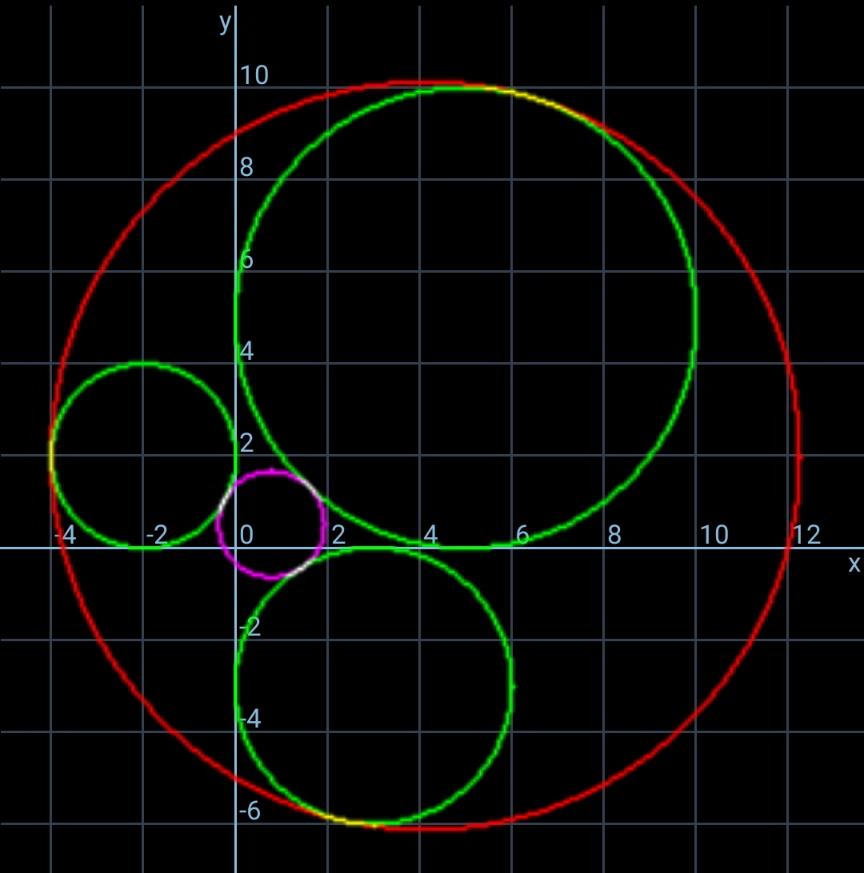
$${Given}\:{three}\:{circles}\:{of}\:{radii}\:{p},\:{q},\:{r} \\ $$$${touching}\:{the}\:{coordinate}\:{axes}\:{as} \\ $$$${shown};\:{find}\:{equation}\:{of}\:{the}\:{circum}- \\ $$$${circle}. \\ $$
Answered by mr W last updated on 09/Jul/20
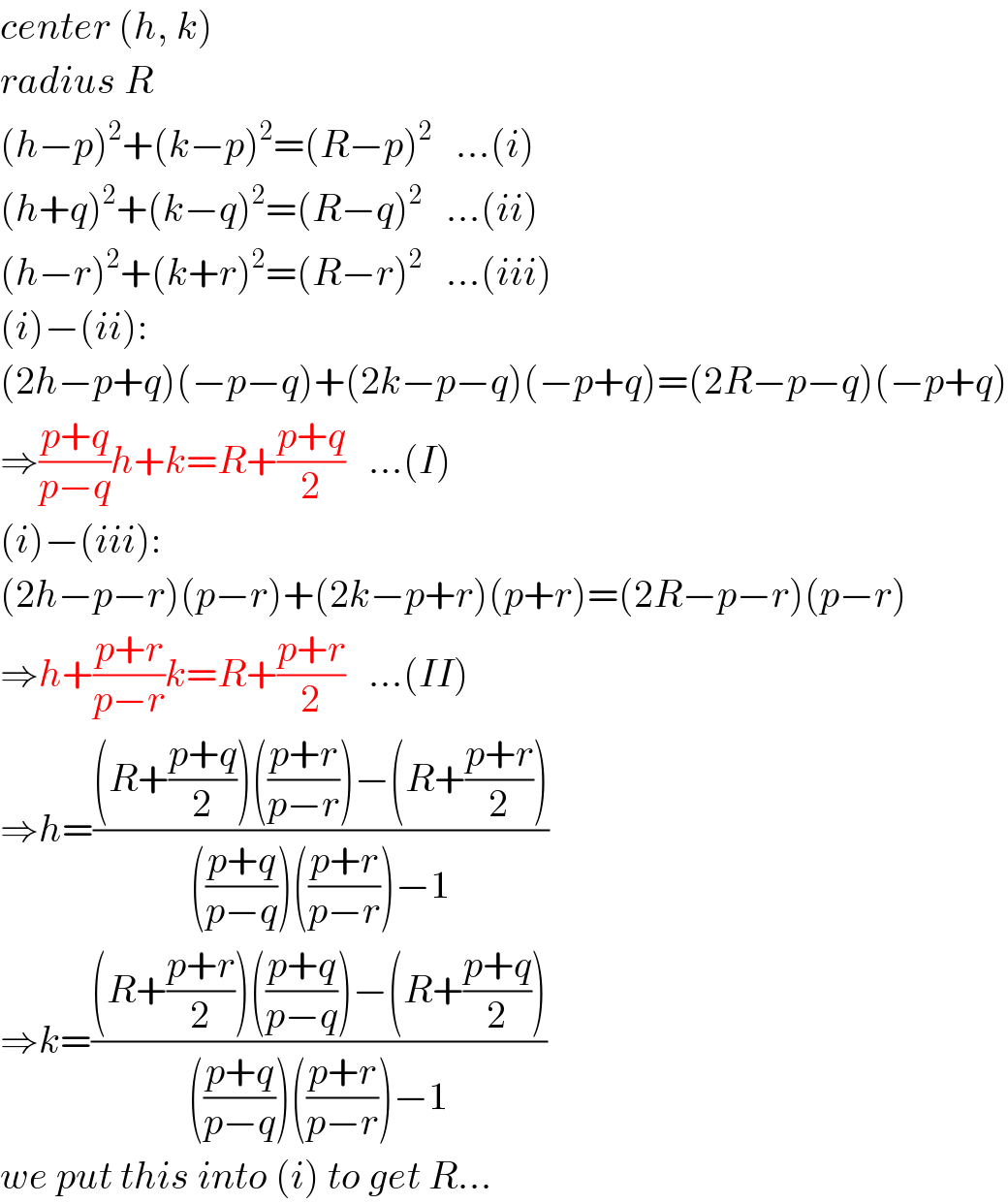
$${center}\:\left({h},\:{k}\right) \\ $$$${radius}\:{R} \\ $$$$\left({h}−{p}\right)^{\mathrm{2}} +\left({k}−{p}\right)^{\mathrm{2}} =\left({R}−{p}\right)^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$$\left({h}+{q}\right)^{\mathrm{2}} +\left({k}−{q}\right)^{\mathrm{2}} =\left({R}−{q}\right)^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$$\left({h}−{r}\right)^{\mathrm{2}} +\left({k}+{r}\right)^{\mathrm{2}} =\left({R}−{r}\right)^{\mathrm{2}} \:\:\:…\left({iii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\left(\mathrm{2}{h}−{p}+{q}\right)\left(−{p}−{q}\right)+\left(\mathrm{2}{k}−{p}−{q}\right)\left(−{p}+{q}\right)=\left(\mathrm{2}{R}−{p}−{q}\right)\left(−{p}+{q}\right) \\ $$$$\Rightarrow\frac{{p}+{q}}{{p}−{q}}{h}+{k}={R}+\frac{{p}+{q}}{\mathrm{2}}\:\:\:…\left({I}\right) \\ $$$$\left({i}\right)−\left({iii}\right): \\ $$$$\left(\mathrm{2}{h}−{p}−{r}\right)\left({p}−{r}\right)+\left(\mathrm{2}{k}−{p}+{r}\right)\left({p}+{r}\right)=\left(\mathrm{2}{R}−{p}−{r}\right)\left({p}−{r}\right) \\ $$$$\Rightarrow{h}+\frac{{p}+{r}}{{p}−{r}}{k}={R}+\frac{{p}+{r}}{\mathrm{2}}\:\:\:…\left({II}\right) \\ $$$$\Rightarrow{h}=\frac{\left({R}+\frac{{p}+{q}}{\mathrm{2}}\right)\left(\frac{{p}+{r}}{{p}−{r}}\right)−\left({R}+\frac{{p}+{r}}{\mathrm{2}}\right)}{\left(\frac{{p}+{q}}{{p}−{q}}\right)\left(\frac{{p}+{r}}{{p}−{r}}\right)−\mathrm{1}} \\ $$$$\Rightarrow{k}=\frac{\left({R}+\frac{{p}+{r}}{\mathrm{2}}\right)\left(\frac{{p}+{q}}{{p}−{q}}\right)−\left({R}+\frac{{p}+{q}}{\mathrm{2}}\right)}{\left(\frac{{p}+{q}}{{p}−{q}}\right)\left(\frac{{p}+{r}}{{p}−{r}}\right)−\mathrm{1}} \\ $$$${we}\:{put}\:{this}\:{into}\:\left({i}\right)\:{to}\:{get}\:{R}… \\ $$
Commented by mr W last updated on 09/Jul/20
Commented by ajfour last updated on 10/Jul/20

$${Straight}\:{enough}\:{Sir},\:{thanks} \\ $$$${a}\:{lot},\:{i}\:{have}\:{no}\:{better}\:{way}.. \\ $$
