Question Number 102544 by 175mohamed last updated on 09/Jul/20

Answered by Rio Michael last updated on 10/Jul/20
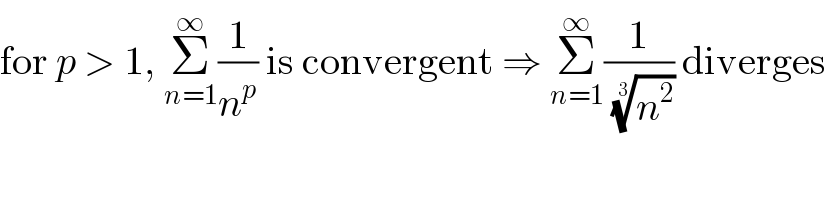
$$\mathrm{for}\:{p}\:>\:\mathrm{1},\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{{p}} }\:\mathrm{is}\:\mathrm{convergent}\:\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }}\:\mathrm{diverges} \\ $$
Answered by mathmax by abdo last updated on 10/Jul/20
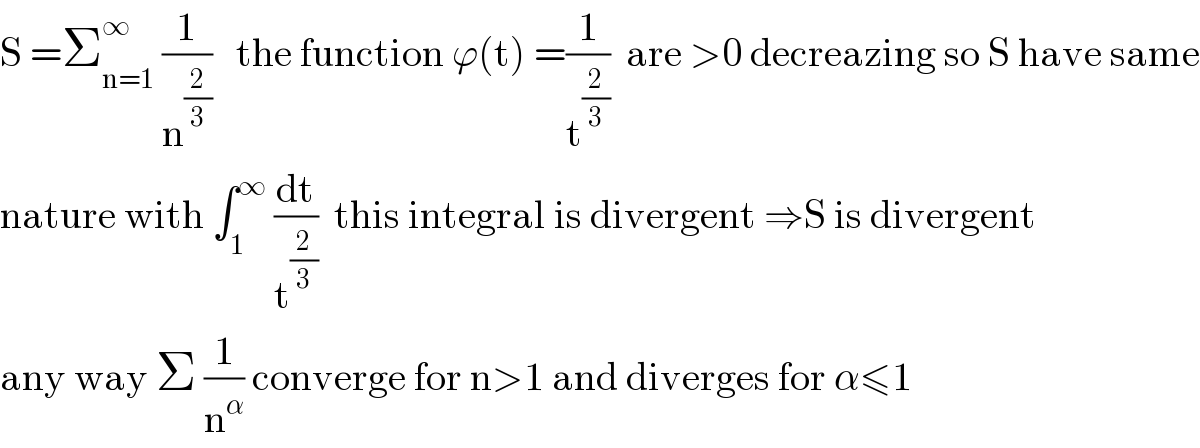
$$\mathrm{S}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:\:\:\mathrm{the}\:\mathrm{function}\:\varphi\left(\mathrm{t}\right)\:=\frac{\mathrm{1}}{\mathrm{t}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:\:\mathrm{are}\:>\mathrm{0}\:\mathrm{decreazing}\:\mathrm{so}\:\mathrm{S}\:\mathrm{have}\:\mathrm{same} \\ $$$$\mathrm{nature}\:\mathrm{with}\:\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:\:\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{divergent}\:\Rightarrow\mathrm{S}\:\mathrm{is}\:\mathrm{divergent} \\ $$$$\mathrm{any}\:\mathrm{way}\:\Sigma\:\frac{\mathrm{1}}{\mathrm{n}^{\alpha} }\:\mathrm{converge}\:\mathrm{for}\:\mathrm{n}>\mathrm{1}\:\mathrm{and}\:\mathrm{diverges}\:\mathrm{for}\:\alpha\leqslant\mathrm{1} \\ $$
Commented by 175mohamed last updated on 13/Jul/20

