Question-102653

Question Number 102653 by Sontsaronald last updated on 10/Jul/20

Answered by bemath last updated on 10/Jul/20

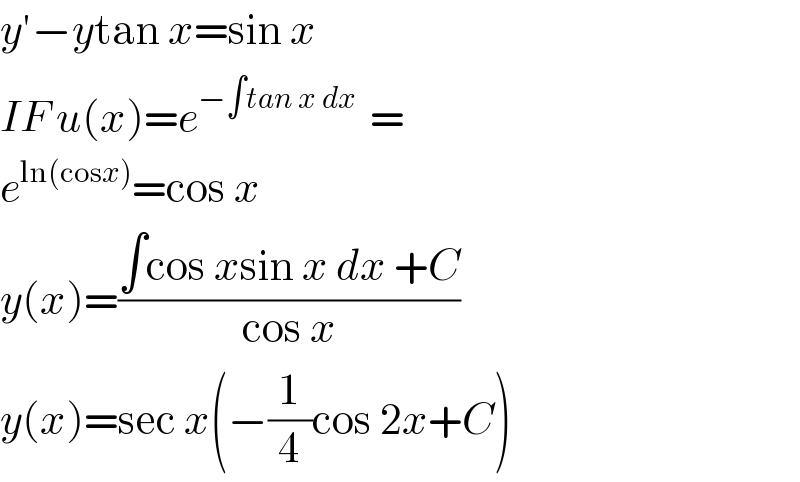
y′−ytan x=sin x IF u(x)=e^(−∫tan x dx ) = e^(ln(cosx)) =cos x y(x)=((∫cos xsin x dx +C)/(cos x)) y(x)=sec x(−(1/4)cos 2x+C)

$${y}'−{y}\mathrm{tan}\:{x}=\mathrm{sin}\:{x} \\ $$$${IF}\:{u}\left({x}\right)={e}^{−\int{tan}\:{x}\:{dx}\:} \:= \\ $$$${e}^{\mathrm{ln}\left(\mathrm{cos}{x}\right)} =\mathrm{cos}\:{x} \\ $$$${y}\left({x}\right)=\frac{\int\mathrm{cos}\:{x}\mathrm{sin}\:{x}\:{dx}\:+{C}}{\mathrm{cos}\:{x}} \\ $$$${y}\left({x}\right)=\mathrm{sec}\:{x}\left(−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{2}{x}+{C}\right) \\ $$

Answered by Ar Brandon last updated on 10/Jul/20

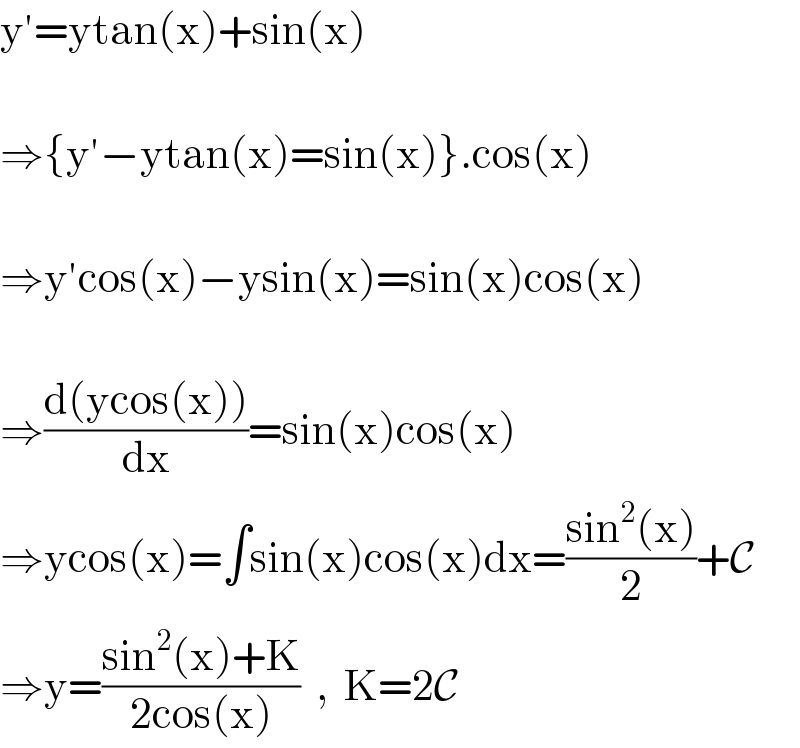
y′=ytan(x)+sin(x) ⇒{y′−ytan(x)=sin(x)}.cos(x) ⇒y′cos(x)−ysin(x)=sin(x)cos(x) ⇒((d(ycos(x)))/dx)=sin(x)cos(x) ⇒ycos(x)=∫sin(x)cos(x)dx=((sin^2 (x))/2)+C ⇒y=((sin^2 (x)+K)/(2cos(x))) , K=2C

$$\mathrm{y}'=\mathrm{ytan}\left(\mathrm{x}\right)+\mathrm{sin}\left(\mathrm{x}\right) \\ $$$$ \\ $$$$\Rightarrow\left\{\mathrm{y}'−\mathrm{ytan}\left(\mathrm{x}\right)=\mathrm{sin}\left(\mathrm{x}\right)\right\}.\mathrm{cos}\left(\mathrm{x}\right) \\ $$$$ \\ $$$$\Rightarrow\mathrm{y}'\mathrm{cos}\left(\mathrm{x}\right)−\mathrm{ysin}\left(\mathrm{x}\right)=\mathrm{sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{x}\right) \\ $$$$ \\ $$$$\Rightarrow\frac{\mathrm{d}\left(\mathrm{ycos}\left(\mathrm{x}\right)\right)}{\mathrm{dx}}=\mathrm{sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{ycos}\left(\mathrm{x}\right)=\int\mathrm{sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{x}\right)\mathrm{dx}=\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{2}}+\mathcal{C} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{K}}{\mathrm{2cos}\left(\mathrm{x}\right)}\:\:,\:\:\mathrm{K}=\mathrm{2}\mathcal{C} \\ $$

Commented by Sontsaronald last updated on 10/Jul/20

$${merci}\:{beaucoup} \\ $$

Commented by Sontsaronald last updated on 10/Jul/20

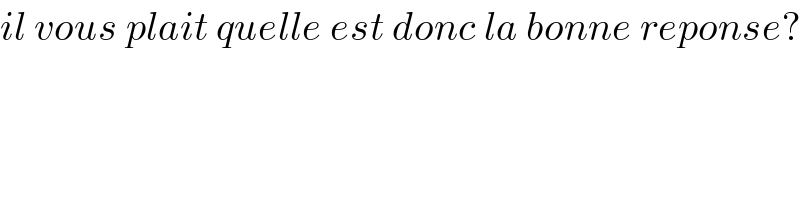
$${il}\:{vous}\:{plait}\:{quelle}\:{est}\:{donc}\:{la}\:{bonne}\:{reponse}? \\ $$

Commented by prakash jain last updated on 10/Jul/20

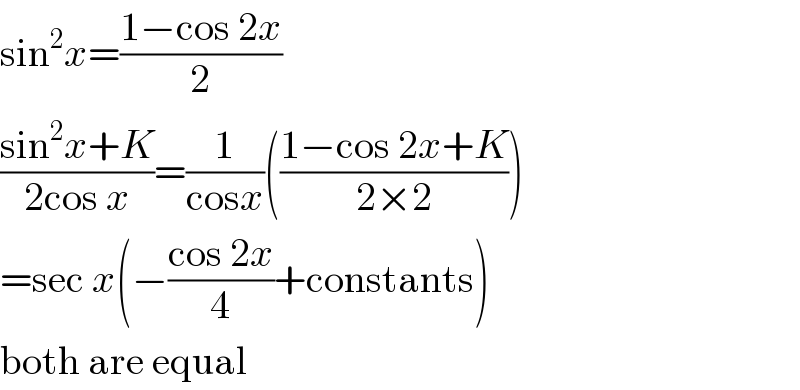
sin^2 x=((1−cos 2x)/2) ((sin^2 x+K)/(2cos x))=(1/(cosx))(((1−cos 2x+K)/(2×2))) =sec x(−((cos 2x)/4)+constants) both are equal

$$\mathrm{sin}^{\mathrm{2}} {x}=\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}} \\ $$$$\frac{\mathrm{sin}^{\mathrm{2}} {x}+{K}}{\mathrm{2cos}\:{x}}=\frac{\mathrm{1}}{\mathrm{cos}{x}}\left(\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}+{K}}{\mathrm{2}×\mathrm{2}}\right) \\ $$$$=\mathrm{sec}\:{x}\left(−\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{4}}+\mathrm{constants}\right) \\ $$$$\mathrm{both}\:\mathrm{are}\:\mathrm{equal} \\ $$

Commented by Ar Brandon last updated on 10/Jul/20

Je vous en prie �� Les deux réponses sont les mêmes, comme vient de le prouver ce monsieur.��

Commented by Ar Brandon last updated on 10/Jul/20

��

Commented by Sontsaronald last updated on 10/Jul/20

$${merci}\:{beaucoup}\:{ohhh} \\ $$

Commented by Ar Brandon last updated on 10/Jul/20

Cette expression ! �� Ça me rappelle de quelqu'un.

Answered by mathmax by abdo last updated on 11/Jul/20

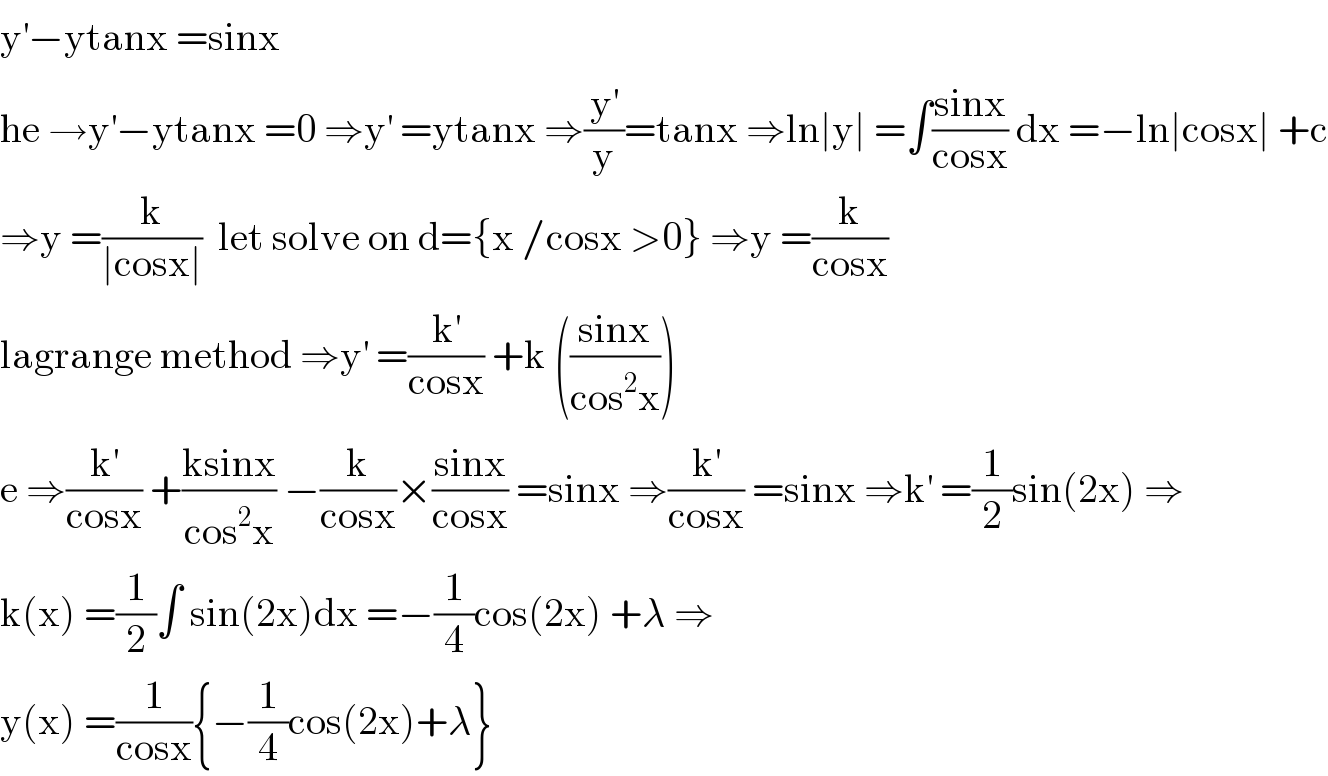
y^′ −ytanx =sinx he →y^′ −ytanx =0 ⇒y^′ =ytanx ⇒(y^′ /y)=tanx ⇒ln∣y∣ =∫((sinx)/(cosx)) dx =−ln∣cosx∣ +c ⇒y =(k/(∣cosx∣)) let solve on d={x /cosx >0} ⇒y =(k/(cosx)) lagrange method ⇒y^′ =(k^′ /(cosx)) +k (((sinx)/(cos^2 x))) e ⇒(k^′ /(cosx)) +((ksinx)/(cos^2 x)) −(k/(cosx))×((sinx)/(cosx)) =sinx ⇒(k^′ /(cosx)) =sinx ⇒k^′ =(1/2)sin(2x) ⇒ k(x) =(1/2)∫ sin(2x)dx =−(1/4)cos(2x) +λ ⇒ y(x) =(1/(cosx)){−(1/4)cos(2x)+λ}

$$\mathrm{y}^{'} −\mathrm{ytanx}\:=\mathrm{sinx} \\ $$$$\mathrm{he}\:\rightarrow\mathrm{y}^{'} −\mathrm{ytanx}\:=\mathrm{0}\:\Rightarrow\mathrm{y}^{'} \:=\mathrm{ytanx}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}=\mathrm{tanx}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=\int\frac{\mathrm{sinx}}{\mathrm{cosx}}\:\mathrm{dx}\:=−\mathrm{ln}\mid\mathrm{cosx}\mid\:+\mathrm{c} \\ $$$$\Rightarrow\mathrm{y}\:=\frac{\mathrm{k}}{\mid\mathrm{cosx}\mid}\:\:\mathrm{let}\:\mathrm{solve}\:\mathrm{on}\:\mathrm{d}=\left\{\mathrm{x}\:/\mathrm{cosx}\:>\mathrm{0}\right\}\:\Rightarrow\mathrm{y}\:=\frac{\mathrm{k}}{\mathrm{cosx}} \\ $$$$\mathrm{lagrange}\:\mathrm{method}\:\Rightarrow\mathrm{y}^{'} \:=\frac{\mathrm{k}^{'} }{\mathrm{cosx}}\:+\mathrm{k}\:\left(\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\right) \\ $$$$\mathrm{e}\:\Rightarrow\frac{\mathrm{k}^{'} }{\mathrm{cosx}}\:+\frac{\mathrm{ksinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:−\frac{\mathrm{k}}{\mathrm{cosx}}×\frac{\mathrm{sinx}}{\mathrm{cosx}}\:=\mathrm{sinx}\:\Rightarrow\frac{\mathrm{k}^{'} }{\mathrm{cosx}}\:=\mathrm{sinx}\:\Rightarrow\mathrm{k}^{'} \:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)\:\Rightarrow \\ $$$$\mathrm{k}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{sin}\left(\mathrm{2x}\right)\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{2x}\right)\:+\lambda\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{cosx}}\left\{−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{2x}\right)+\lambda\right\} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply