Menu Close

Question-102978

Tinku Tara 0 Comments
Pin




Question Number 102978 by ajfour last updated on 12/Jul/20
Commented by ajfour last updated on 12/Jul/20
The inclined plane of mass m, length L and the block of mass m, both are on the verge of slipping. Find x and μ.
$${The}\:{inclined}\:{plane}\:{of}\:{mass}\:{m}, \\ $$$${length}\:{L}\:{and}\:{the}\:{block}\:{of}\:{mass}\:{m}, \\ $$$${both}\:{are}\:{on}\:{the}\:{verge}\:{of}\:{slipping}. \\ $$$${Find}\:{x}\:{and}\:\mu. \\ $$
Answered by mr W last updated on 12/Jul/20
Commented by mr W last updated on 12/Jul/20
x=L sin θ C=center of total mass of both objects M=2m BC=p=((mx+m×(L/2))/(2m))=((L(2 sin θ+1))/4) CA=q=L−p=((L(3−2 sin θ))/4) tan φ=μ such that the block m doesn′t slip, tan θ=μ ⇒φ=θ α=(π/2)−θ−φ=(π/2)−2θ β=φ+θ=2θ ((SC)/(sin β))=((BC)/(sin ((π/2)−φ)))=(p/(cos θ)) ⇒SC=((p sin β)/(cos θ))=((L(2 sin θ+1) sin 2θ)/(4 cos θ)) =((L(2 sin θ+1) sin θ)/2) ((SC)/(sin α))=((CA)/(sin φ))=(q/(sin θ)) ⇒SC=((q sin α)/(sin θ))=((L(3−2 sin θ) cos 2θ)/(4 sin θ)) ((L(3−2 sin θ) cos 2θ)/(4 sin θ))=((L(2 sin θ+1) sin θ)/2) ⇒8 sin^2 θ+2 sin θ−3=0 ⇒(2 sin θ−1)(4 sin θ+3)=0 ⇒sin θ=(x/L)=(1/2) or −(3/4) (rejected) ⇒θ=30° ⇒μ=tan θ=(1/( (√3)))
$${x}={L}\:\mathrm{sin}\:\theta \\ $$$${C}={center}\:{of}\:{total}\:{mass}\:{of}\:{both}\:{objects} \\ $$$${M}=\mathrm{2}{m} \\ $$$${BC}={p}=\frac{{mx}+{m}×\frac{{L}}{\mathrm{2}}}{\mathrm{2}{m}}=\frac{{L}\left(\mathrm{2}\:\mathrm{sin}\:\theta+\mathrm{1}\right)}{\mathrm{4}} \\ $$$${CA}={q}={L}−{p}=\frac{{L}\left(\mathrm{3}−\mathrm{2}\:\mathrm{sin}\:\theta\right)}{\mathrm{4}} \\ $$$$\mathrm{tan}\:\phi=\mu \\ $$$${such}\:{that}\:{the}\:{block}\:{m}\:{doesn}'{t}\:{slip}, \\ $$$$\mathrm{tan}\:\theta=\mu \\ $$$$\Rightarrow\phi=\theta \\ $$$$\alpha=\frac{\pi}{\mathrm{2}}−\theta−\phi=\frac{\pi}{\mathrm{2}}−\mathrm{2}\theta \\ $$$$\beta=\phi+\theta=\mathrm{2}\theta \\ $$$$\frac{{SC}}{\mathrm{sin}\:\beta}=\frac{{BC}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\phi\right)}=\frac{{p}}{\mathrm{cos}\:\theta} \\ $$$$\Rightarrow{SC}=\frac{{p}\:\mathrm{sin}\:\beta}{\mathrm{cos}\:\theta}=\frac{{L}\left(\mathrm{2}\:\mathrm{sin}\:\theta+\mathrm{1}\right)\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{4}\:\mathrm{cos}\:\theta} \\ $$$$=\frac{{L}\left(\mathrm{2}\:\mathrm{sin}\:\theta+\mathrm{1}\right)\:\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$$\frac{{SC}}{\mathrm{sin}\:\alpha}=\frac{{CA}}{\mathrm{sin}\:\phi}=\frac{{q}}{\mathrm{sin}\:\theta} \\ $$$$\Rightarrow{SC}=\frac{{q}\:\mathrm{sin}\:\alpha}{\mathrm{sin}\:\theta}=\frac{{L}\left(\mathrm{3}−\mathrm{2}\:\mathrm{sin}\:\theta\right)\:\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{4}\:\mathrm{sin}\:\theta} \\ $$$$ \\ $$$$\frac{{L}\left(\mathrm{3}−\mathrm{2}\:\mathrm{sin}\:\theta\right)\:\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{4}\:\mathrm{sin}\:\theta}=\frac{{L}\left(\mathrm{2}\:\mathrm{sin}\:\theta+\mathrm{1}\right)\:\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{8}\:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}\:\mathrm{sin}\:\theta−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}\:\mathrm{sin}\:\theta−\mathrm{1}\right)\left(\mathrm{4}\:\mathrm{sin}\:\theta+\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{{x}}{{L}}=\frac{\mathrm{1}}{\mathrm{2}}\:{or}\:−\frac{\mathrm{3}}{\mathrm{4}}\:\left({rejected}\right) \\ $$$$\Rightarrow\theta=\mathrm{30}° \\ $$$$\Rightarrow\mu=\mathrm{tan}\:\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$
Commented by mr W last updated on 12/Jul/20
if block and plane have different masses, say mass of block is λm, and mass of plane is m, then M=(1+λ)m BC=p=((λmx+m×(L/2))/((λ+1)m))=((L(2λ sin θ+1))/(2(λ+1))) CA=q=L−p=((L[1+2λ(1−sin θ)])/(2(λ+1))) ⇒SC=((p sin β)/(cos θ))=((L(2λ sin θ+1) sin θ)/((λ+1))) ⇒SC=((q sin α)/(sin θ))=((L[1+2λ(1−sin θ)]cos 2θ)/(2(λ+1) sin θ)) ((L[1+2λ(1−sin θ)]cos 2θ)/(2(λ+1) sin θ))=((L(2λ sin θ+1) sin θ)/((λ+1))) [1+2λ(1−sin θ)](1−2 sin^2 θ)=2(2λ sin θ+1) sin^2 with t=sin θ 4(λ+1)t^2 +2λt−(2λ+1)=0 t=((−2λ+(√(4λ^2 +16(λ+1)(2λ+1))))/(8(λ+1))) t=((−λ+3λ+2)/(4(λ+1)))=(1/2)=sin θ that means the solution is the same even when both objects have different masses.
$${if}\:{block}\:{and}\:{plane}\:{have}\:{different} \\ $$$${masses},\:{say}\:{mass}\:{of}\:{block}\:{is}\:\lambda{m},\:{and} \\ $$$${mass}\:{of}\:{plane}\:{is}\:{m},\:{then} \\ $$$${M}=\left(\mathrm{1}+\lambda\right){m} \\ $$$${BC}={p}=\frac{\lambda{mx}+{m}×\frac{{L}}{\mathrm{2}}}{\left(\lambda+\mathrm{1}\right){m}}=\frac{{L}\left(\mathrm{2}\lambda\:\mathrm{sin}\:\theta+\mathrm{1}\right)}{\mathrm{2}\left(\lambda+\mathrm{1}\right)} \\ $$$${CA}={q}={L}−{p}=\frac{{L}\left[\mathrm{1}+\mathrm{2}\lambda\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\right]}{\mathrm{2}\left(\lambda+\mathrm{1}\right)} \\ $$$$\Rightarrow{SC}=\frac{{p}\:\mathrm{sin}\:\beta}{\mathrm{cos}\:\theta}=\frac{{L}\left(\mathrm{2}\lambda\:\mathrm{sin}\:\theta+\mathrm{1}\right)\:\mathrm{sin}\:\theta}{\left(\lambda+\mathrm{1}\right)} \\ $$$$\Rightarrow{SC}=\frac{{q}\:\mathrm{sin}\:\alpha}{\mathrm{sin}\:\theta}=\frac{{L}\left[\mathrm{1}+\mathrm{2}\lambda\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\right]\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{2}\left(\lambda+\mathrm{1}\right)\:\mathrm{sin}\:\theta} \\ $$$$\frac{{L}\left[\mathrm{1}+\mathrm{2}\lambda\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\right]\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{2}\left(\lambda+\mathrm{1}\right)\:\mathrm{sin}\:\theta}=\frac{{L}\left(\mathrm{2}\lambda\:\mathrm{sin}\:\theta+\mathrm{1}\right)\:\mathrm{sin}\:\theta}{\left(\lambda+\mathrm{1}\right)} \\ $$$$\left[\mathrm{1}+\mathrm{2}\lambda\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\right]\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)=\mathrm{2}\left(\mathrm{2}\lambda\:\mathrm{sin}\:\theta+\mathrm{1}\right)\:\mathrm{sin}^{\mathrm{2}} \\ $$$${with}\:{t}=\mathrm{sin}\:\theta \\ $$$$\mathrm{4}\left(\lambda+\mathrm{1}\right){t}^{\mathrm{2}} +\mathrm{2}\lambda{t}−\left(\mathrm{2}\lambda+\mathrm{1}\right)=\mathrm{0} \\ $$$${t}=\frac{−\mathrm{2}\lambda+\sqrt{\mathrm{4}\lambda^{\mathrm{2}} +\mathrm{16}\left(\lambda+\mathrm{1}\right)\left(\mathrm{2}\lambda+\mathrm{1}\right)}}{\mathrm{8}\left(\lambda+\mathrm{1}\right)} \\ $$$${t}=\frac{−\lambda+\mathrm{3}\lambda+\mathrm{2}}{\mathrm{4}\left(\lambda+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{sin}\:\theta \\ $$$${that}\:{means}\:{the}\:{solution}\:{is}\:{the}\:{same} \\ $$$${even}\:{when}\:{both}\:{objects}\:{have}\:{different} \\ $$$${masses}. \\ $$
Commented by ajfour last updated on 12/Jul/20
Great! I got chance to understand the principle once again Sir. Thanksfor this viewpoint.
$${Great}!\:\:{I}\:{got}\:{chance}\:{to}\:{understand} \\ $$$${the}\:{principle}\:{once}\:{again}\:{Sir}. \\ $$$${Thanksfor}\:{this}\:{viewpoint}. \\ $$
Commented by ajfour last updated on 12/Jul/20
Nice, what made you suspect so Sir ?
$${Nice},\:{what}\:{made}\:{you}\:{suspect}\:{so} \\ $$$${Sir}\:? \\ $$
Commented by mr W last updated on 12/Jul/20
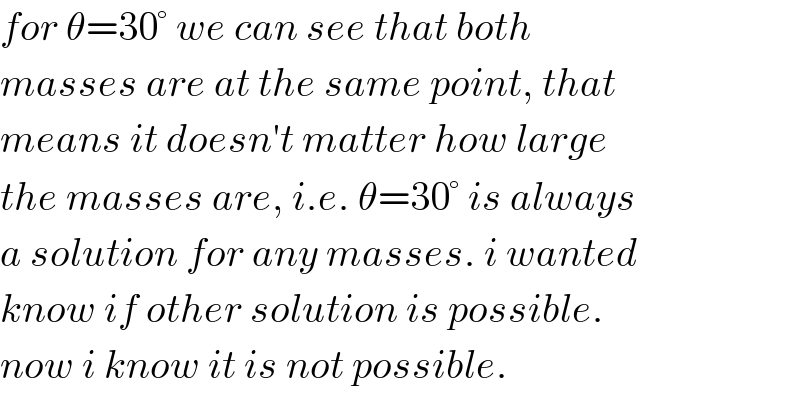
for θ=30° we can see that both masses are at the same point, that means it doesn′t matter how large the masses are, i.e. θ=30° is always a solution for any masses. i wanted know if other solution is possible. now i know it is not possible.
$${for}\:\theta=\mathrm{30}°\:{we}\:{can}\:{see}\:{that}\:{both} \\ $$$${masses}\:{are}\:{at}\:{the}\:{same}\:{point},\:{that} \\ $$$${means}\:{it}\:{doesn}'{t}\:{matter}\:{how}\:{large} \\ $$$${the}\:{masses}\:{are},\:{i}.{e}.\:\theta=\mathrm{30}°\:{is}\:{always} \\ $$$${a}\:{solution}\:{for}\:{any}\:{masses}.\:{i}\:{wanted}\: \\ $$$${know}\:{if}\:{other}\:{solution}\:{is}\:{possible}. \\ $$$${now}\:{i}\:{know}\:{it}\:{is}\:{not}\:{possible}. \\ $$
Answered by ajfour last updated on 12/Jul/20
Commented by ajfour last updated on 12/Jul/20
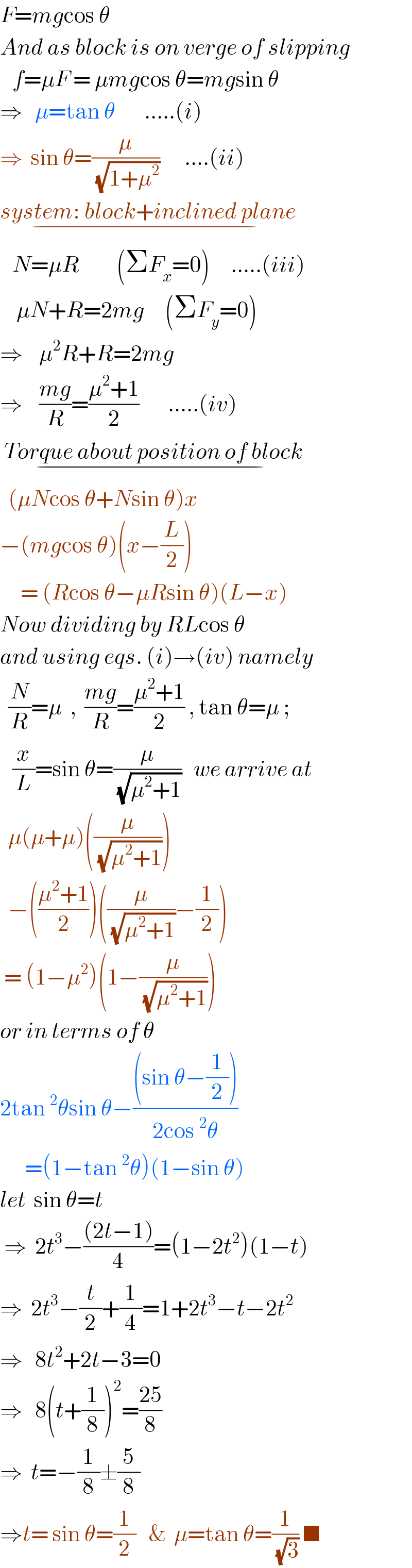
F=mgcos θ And as block is on verge of slipping f=μF = μmgcos θ=mgsin θ ⇒ μ=tan θ .....(i) ⇒ sin θ=(μ/( (√(1+μ^2 )))) ....(ii) system: block+inclined plane_(−) N=μR (ΣF_x =0) .....(iii) μN+R=2mg (ΣF_y =0) ⇒ μ^2 R+R=2mg ⇒ ((mg)/R)=((μ^2 +1)/2) .....(iv) Torque about position of block_(−) (μNcos θ+Nsin θ)x −(mgcos θ)(x−(L/2)) = (Rcos θ−μRsin θ)(L−x) Now dividing by RLcos θ and using eqs. (i)→(iv) namely (N/R)=μ , ((mg)/R)=((μ^2 +1)/2) , tan θ=μ ; (x/L)=sin θ=(μ/( (√(μ^2 +1)))) we arrive at μ(μ+μ)((μ/( (√(μ^2 +1))))) −(((μ^2 +1)/2))((μ/( (√(μ^2 +1))))−(1/2)) = (1−μ^2 )(1−(μ/( (√(μ^2 +1))))) or in terms of θ 2tan^2 θsin θ−(((sin θ−(1/2)))/(2cos^2 θ)) =(1−tan^2 θ)(1−sin θ) let sin θ=t ⇒ 2t^3 −(((2t−1))/4)=(1−2t^2 )(1−t) ⇒ 2t^3 −(t/2)+(1/4)=1+2t^3 −t−2t^2 ⇒ 8t^2 +2t−3=0 ⇒ 8(t+(1/8))^2 =((25)/8) ⇒ t=−(1/8)±(5/8) ⇒t= sin θ=(1/2) & μ=tan θ=(1/( (√3))) ■
$${F}={mg}\mathrm{cos}\:\theta \\ $$$${And}\:{as}\:{block}\:{is}\:{on}\:{verge}\:{of}\:{slipping} \\ $$$$\:\:\:{f}=\mu{F}\:=\:\mu{mg}\mathrm{cos}\:\theta={mg}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\:\mu=\mathrm{tan}\:\theta\:\:\:\:\:\:\:…..\left({i}\right) \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\theta=\frac{\mu}{\:\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }}\:\:\:\:\:\:….\left({ii}\right) \\ $$$$\underset{−} {{system}:\:{block}+{inclined}\:{plane}} \\ $$$$\:\:\:{N}=\mu{R}\:\:\:\:\:\:\:\:\:\left(\Sigma{F}_{{x}} =\mathrm{0}\right)\:\:\:\:\:…..\left({iii}\right) \\ $$$$\:\:\:\:\mu{N}+{R}=\mathrm{2}{mg}\:\:\:\:\:\left(\Sigma{F}_{{y}} =\mathrm{0}\right) \\ $$$$\Rightarrow\:\:\:\:\mu^{\mathrm{2}} {R}+{R}=\mathrm{2}{mg} \\ $$$$\Rightarrow\:\:\:\:\frac{{mg}}{{R}}=\frac{\mu^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:…..\left({iv}\right) \\ $$$$\:\underset{−} {{Torque}\:{about}\:{position}\:{of}\:{block}} \\ $$$$\:\:\left(\mu{N}\mathrm{cos}\:\theta+{N}\mathrm{sin}\:\theta\right){x} \\ $$$$−\left({mg}\mathrm{cos}\:\theta\right)\left({x}−\frac{{L}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:=\:\left({R}\mathrm{cos}\:\theta−\mu{R}\mathrm{sin}\:\theta\right)\left({L}−{x}\right) \\ $$$${Now}\:{dividing}\:{by}\:{RL}\mathrm{cos}\:\theta \\ $$$${and}\:{using}\:{eqs}.\:\left({i}\right)\rightarrow\left({iv}\right)\:{namely} \\ $$$$\:\:\frac{{N}}{{R}}=\mu\:\:,\:\:\frac{{mg}}{{R}}=\frac{\mu^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}}\:,\:\mathrm{tan}\:\theta=\mu\:; \\ $$$$\:\:\:\frac{{x}}{{L}}=\mathrm{sin}\:\theta=\frac{\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{1}}}\:\:\:{we}\:{arrive}\:{at} \\ $$$$\:\:\mu\left(\mu+\mu\right)\left(\frac{\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{1}}}\right) \\ $$$$\:\:−\left(\frac{\mu^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{1}}}−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:=\:\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\left(\mathrm{1}−\frac{\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{1}}}\right) \\ $$$${or}\:{in}\:{terms}\:{of}\:\theta \\ $$$$\mathrm{2tan}\:^{\mathrm{2}} \theta\mathrm{sin}\:\theta−\frac{\left(\mathrm{sin}\:\theta−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2cos}\:^{\mathrm{2}} \theta} \\ $$$$\:\:\:\:\:\:=\left(\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \theta\right)\left(\mathrm{1}−\mathrm{sin}\:\theta\right) \\ $$$${let}\:\:\mathrm{sin}\:\theta={t} \\ $$$$\:\Rightarrow\:\:\mathrm{2}{t}^{\mathrm{3}} −\frac{\left(\mathrm{2}{t}−\mathrm{1}\right)}{\mathrm{4}}=\left(\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} \right)\left(\mathrm{1}−{t}\right) \\ $$$$\Rightarrow\:\:\mathrm{2}{t}^{\mathrm{3}} −\frac{{t}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{1}+\mathrm{2}{t}^{\mathrm{3}} −{t}−\mathrm{2}{t}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\mathrm{8}{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{8}\left({t}+\frac{\mathrm{1}}{\mathrm{8}}\right)^{\mathrm{2}} =\frac{\mathrm{25}}{\mathrm{8}} \\ $$$$\Rightarrow\:\:{t}=−\frac{\mathrm{1}}{\mathrm{8}}\pm\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\Rightarrow{t}=\:\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\&\:\:\mu=\mathrm{tan}\:\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\blacksquare \\ $$
Commented by mr W last updated on 12/Jul/20
wonderful solution sir!
$${wonderful}\:{solution}\:{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *