Question Number 102980 by ajfour last updated on 12/Jul/20
Commented by ajfour last updated on 12/Jul/20

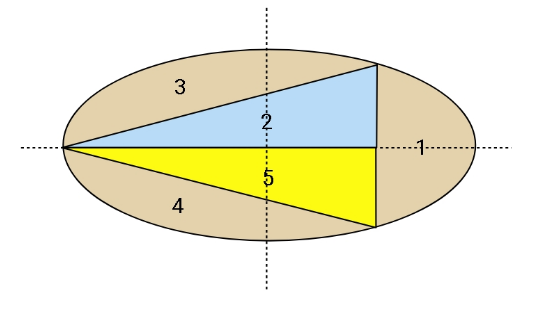
$${Find}\:\:{a}/{b}\:\:{if}\:{regions}\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5} \\ $$$${have}\:{equal}\:{areas}. \\ $$
Commented by mr W last updated on 12/Jul/20
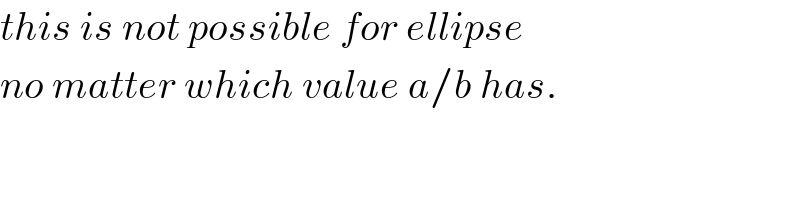
$${this}\:{is}\:{not}\:{possible}\:{for}\:{ellipse} \\ $$$${no}\:{matter}\:{which}\:{value}\:{a}/{b}\:{has}. \\ $$
Commented by mr W last updated on 12/Jul/20

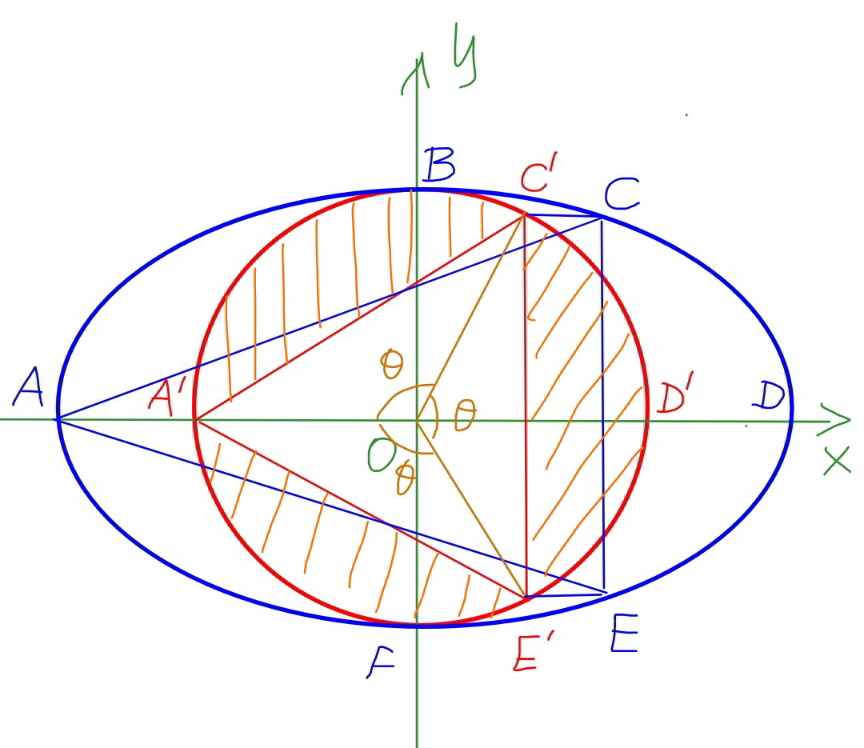
$${if}\:{this}\:{is}\:{true},\:{say}\:{for}\:{a}\:{certain} \\ $$$${value}\:{of}\:{a}/{b},\:{then}\:{it}\:{must}\:{be}\:{also}\:{true} \\ $$$${when}\:{we}\:{shrink}\:{the}\:{ellipse}\:{in} \\ $$$${x}−{direction}\:{in}\:{ratio}\:{b}/{a}\:{to}\:{a}\:{circle} \\ $$$${with}\:{radius}\:{r}={b}. \\ $$$${that}\:{means}\:{each}\:{of}\:{the}\:{three}\:{shaded} \\ $$$${segments}\:{of}\:{the}\:{circle}\:{must}\:{have}\: \\ $$$${fifth}\:{of}\:{the}\:{area}\:{of}\:{the}\:{circle}.\:{but} \\ $$$${this}\:{is}\:{not}\:{possible},\:{since} \\ $$$${area}\:{of}\:{segement}\:=\frac{{b}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\neq\frac{\pi{b}^{\mathrm{2}} }{\mathrm{5}} \\ $$
Commented by mr W last updated on 12/Jul/20
Commented by ajfour last updated on 12/Jul/20

$$''\:\:{then}\:{it}\:{must}\:{be}\:{also}\:{true} \\ $$$${when}\:{we}\:{shrink}\:{the}\:{ellipse}\:'' \\ $$$$\:\:\:\:\:{may}\:{not}\:{necessarily}\:{be}\:{true} \\ $$$$\:\:\:\:\:{Sir}…. \\ $$
Commented by mr W last updated on 12/Jul/20

$${when}\:{an}\:{ellipse}\:{is}\:{shrinked}\:{in} \\ $$$${x}−{direction}\:{in}\:{ratio}\:\frac{{b}}{{a}},\:{the}\:{area}\:{of} \\ $$$${each}\:{part}\:{is}\:{shrinked}\:{in}\:{the}\:{same} \\ $$$${ratio}\:\frac{{b}}{{a}}: \\ $$$${A}_{\mathrm{1}} \:\rightarrow{A}_{\mathrm{1}} ^{'} =\frac{{b}}{{a}}{A}_{\mathrm{1}} \\ $$$${A}_{\mathrm{2}} \:\rightarrow{A}_{\mathrm{2}} ^{'} =\frac{{b}}{{a}}{A}_{\mathrm{2}} \\ $$$$… \\ $$$${therefore}\:{if}\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} ={A}_{\mathrm{3}} =…,\:{we}\:{get} \\ $$$${also}\:{A}_{\mathrm{1}} '={A}_{\mathrm{2}} '={A}_{\mathrm{3}} '=… \\ $$
Answered by ajfour last updated on 12/Jul/20
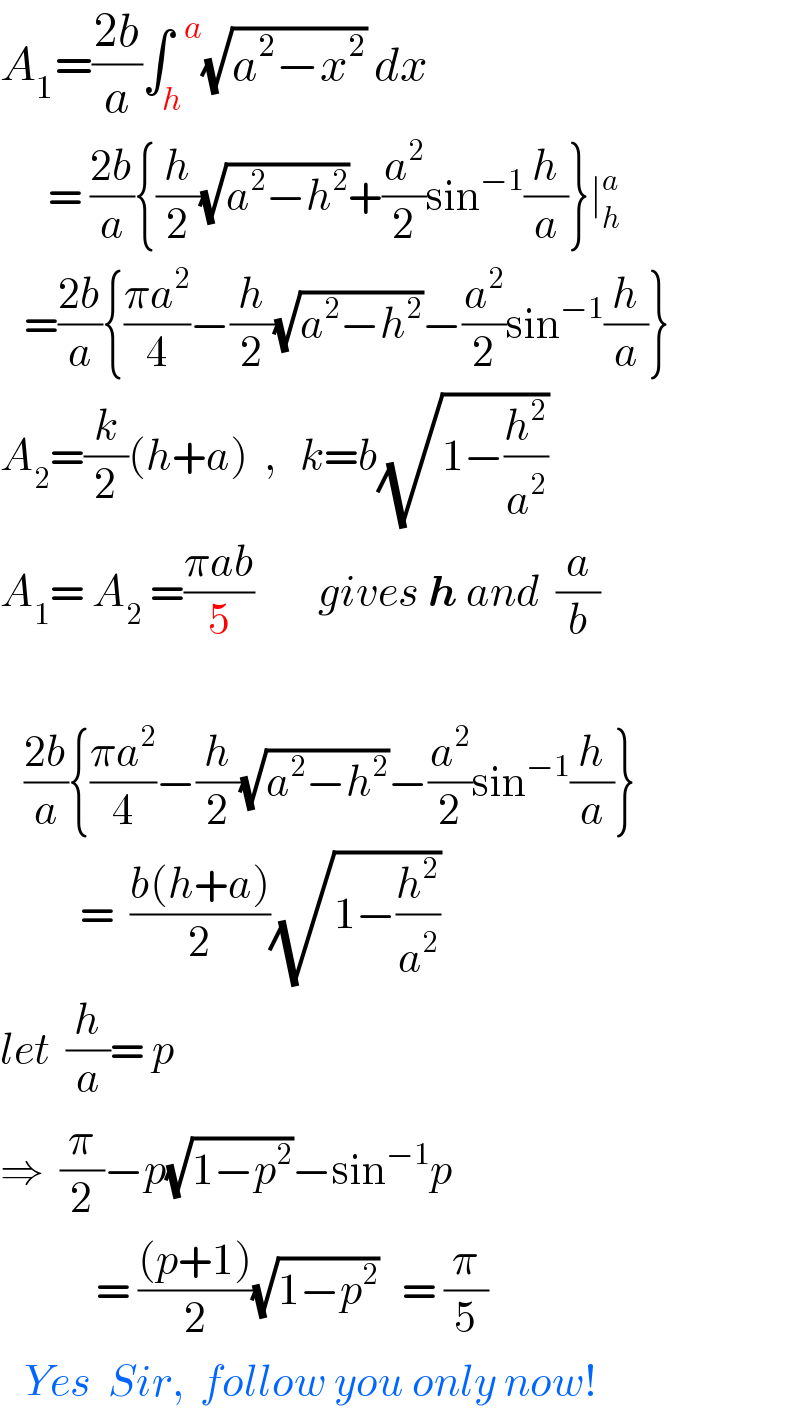
$${A}_{\mathrm{1}} =\frac{\mathrm{2}{b}}{{a}}\int_{{h}} ^{\:\:{a}} \sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:{dx} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{2}{b}}{{a}}\left\{\frac{{h}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{h}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{{h}}{{a}}\right\}\mid_{{h}} ^{{a}} \\ $$$$\:\:\:=\frac{\mathrm{2}{b}}{{a}}\left\{\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}−\frac{{h}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{h}^{\mathrm{2}} }−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{{h}}{{a}}\right\} \\ $$$${A}_{\mathrm{2}} =\frac{{k}}{\mathrm{2}}\left({h}+{a}\right)\:\:,\:\:\:{k}={b}\sqrt{\mathrm{1}−\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \\ $$$${A}_{\mathrm{1}} =\:{A}_{\mathrm{2}} \:=\frac{\pi{ab}}{\mathrm{5}}\:\:\:\:\:\:\:\:{gives}\:\boldsymbol{{h}}\:{and}\:\:\frac{{a}}{{b}}\: \\ $$$$ \\ $$$$\:\:\:\frac{\mathrm{2}{b}}{{a}}\left\{\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}−\frac{{h}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{h}^{\mathrm{2}} }−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{{h}}{{a}}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\:\frac{{b}\left({h}+{a}\right)}{\mathrm{2}}\sqrt{\mathrm{1}−\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \\ $$$${let}\:\:\frac{{h}}{{a}}=\:{p} \\ $$$$\Rightarrow\:\:\frac{\pi}{\mathrm{2}}−{p}\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }−\mathrm{sin}^{−\mathrm{1}} {p} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\left({p}+\mathrm{1}\right)}{\mathrm{2}}\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\:\:\:=\:\frac{\pi}{\mathrm{5}} \\ $$$$\:\:\:{Yes}\:\:{Sir},\:\:{follow}\:{you}\:{only}\:{now}! \\ $$
Commented by mr W last updated on 12/Jul/20

$${you}\:{can}\:{make}\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} \:{or}\:{A}_{\mathrm{1}} ={A}_{\mathrm{3}} \:{or} \\ $$$${A}_{\mathrm{2}} ={A}_{\mathrm{3}} \:{for}\:{any}\:{ellipse},\:{but}\:{never} \\ $$$${A}_{\mathrm{1}} ={A}_{\mathrm{2}} ={A}_{\mathrm{3}} . \\ $$
Commented by ajfour last updated on 12/Jul/20
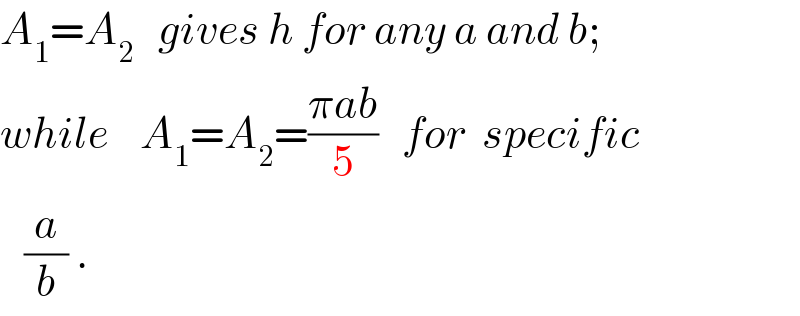
$${A}_{\mathrm{1}} ={A}_{\mathrm{2}} \:\:\:{gives}\:{h}\:{for}\:{any}\:{a}\:{and}\:{b}; \\ $$$${while}\:\:\:\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} =\frac{\pi{ab}}{\mathrm{5}}\:\:\:{for}\:\:{specific} \\ $$$$\:\:\:\frac{{a}}{{b}}\:. \\ $$
Commented by mr W last updated on 12/Jul/20
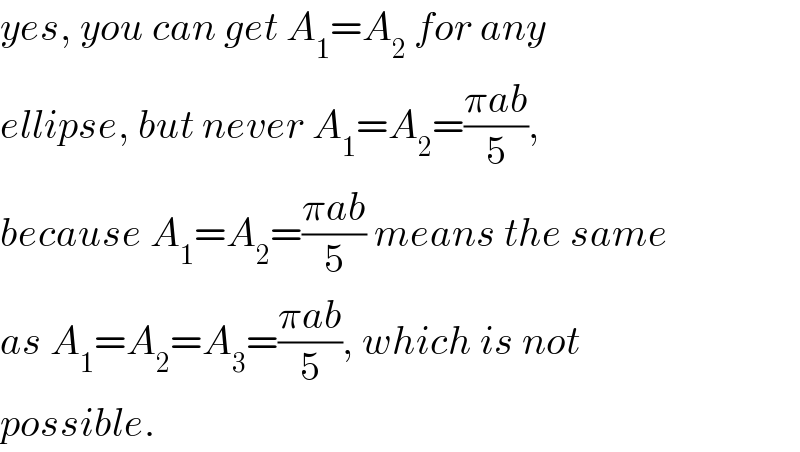
$${yes},\:{you}\:{can}\:{get}\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} \:{for}\:{any} \\ $$$${ellipse},\:{but}\:{never}\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} =\frac{\pi{ab}}{\mathrm{5}}, \\ $$$${because}\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} =\frac{\pi{ab}}{\mathrm{5}}\:{means}\:{the}\:{same} \\ $$$${as}\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} ={A}_{\mathrm{3}} =\frac{\pi{ab}}{\mathrm{5}},\:{which}\:{is}\:{not} \\ $$$${possible}. \\ $$
