Question Number 103062 by ajfour last updated on 12/Jul/20
Commented by ajfour last updated on 12/Jul/20

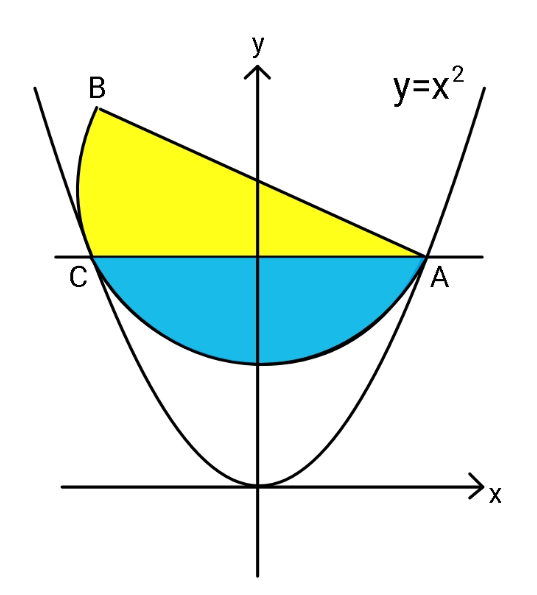
$${If}\:{both}\:{coloured}\:{regions}\:{have} \\ $$$${equal}\:{areas},\:{find}\:{radius}\:{of}\:{the} \\ $$$${semicircle}. \\ $$
Answered by mr W last updated on 12/Jul/20

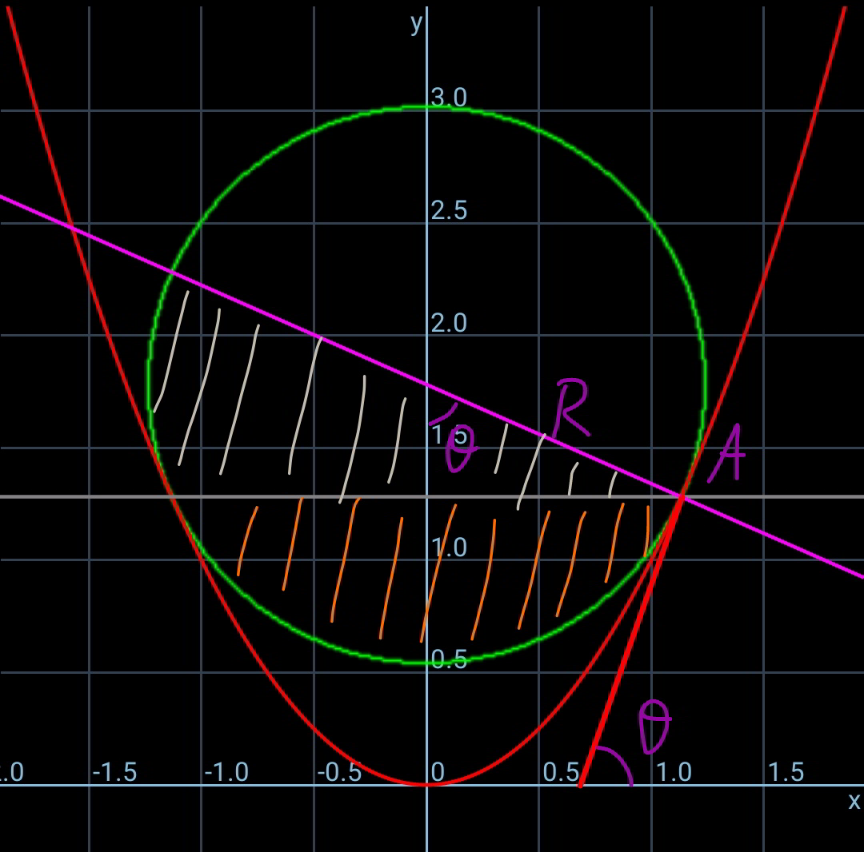
$${area}\:{of}\:{segment}: \\ $$$$\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\theta−\mathrm{sin}\:\mathrm{2}\theta\right)=\frac{\pi{R}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{2}\theta−\mathrm{sin}\:\mathrm{2}\theta=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\mathrm{1}.\mathrm{1549}\:\left(=\mathrm{66}.\mathrm{17}°\right) \\ $$$$ \\ $$$$\mathrm{tan}\:\theta={y}'=\mathrm{2}{R}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{R}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\theta}\approx\mathrm{1}.\mathrm{2376} \\ $$
Commented by mr W last updated on 12/Jul/20
Commented by ajfour last updated on 12/Jul/20
$${Short},\:{succinct}\:{and}\:{Nice}\:{Sir}! \\ $$
