Question Number 103094 by I want to learn more last updated on 12/Jul/20

$$. \\ $$
Commented by I want to learn more last updated on 12/Jul/20
The area of a circle is increasing at the rate of 4cm²/s. Find the rate of change of the circumference when the radius is 6cm.
Commented by I want to learn more last updated on 12/Jul/20
$$\mathrm{Please}\:\mathrm{workings}\:\mathrm{sir} \\ $$
Commented by Dwaipayan Shikari last updated on 12/Jul/20
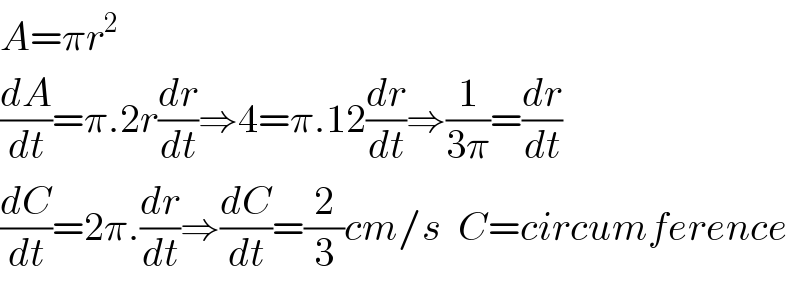
$${A}=\pi{r}^{\mathrm{2}} \\ $$$$\frac{{dA}}{{dt}}=\pi.\mathrm{2}{r}\frac{{dr}}{{dt}}\Rightarrow\mathrm{4}=\pi.\mathrm{12}\frac{{dr}}{{dt}}\Rightarrow\frac{\mathrm{1}}{\mathrm{3}\pi}=\frac{{dr}}{{dt}} \\ $$$$\frac{{dC}}{{dt}}=\mathrm{2}\pi.\frac{{dr}}{{dt}}\Rightarrow\frac{{dC}}{{dt}}=\frac{\mathrm{2}}{\mathrm{3}}{cm}/{s}\:\:{C}={circumference} \\ $$
Commented by I want to learn more last updated on 14/Jul/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
