Question Number 103165 by ajfour last updated on 13/Jul/20
Commented by ajfour last updated on 13/Jul/20

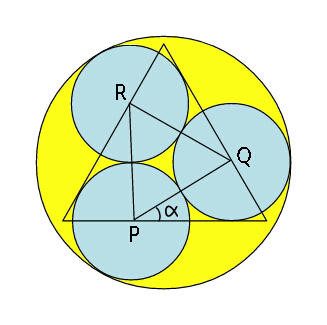
$${If}\:{outer}\:{circle}\:{has}\:{unit}\:{radius}, \\ $$$${find}\:{side}\:{of}\:{the}\:{equilateral}\:\bigtriangleup. \\ $$$${P},\:{Q},{R}\:{are}\:{centres}\:{of}\:{the}\: \\ $$$${smaller}\:{circles}.\:{Also}\:{find}\:\alpha. \\ $$
Commented by mr W last updated on 13/Jul/20
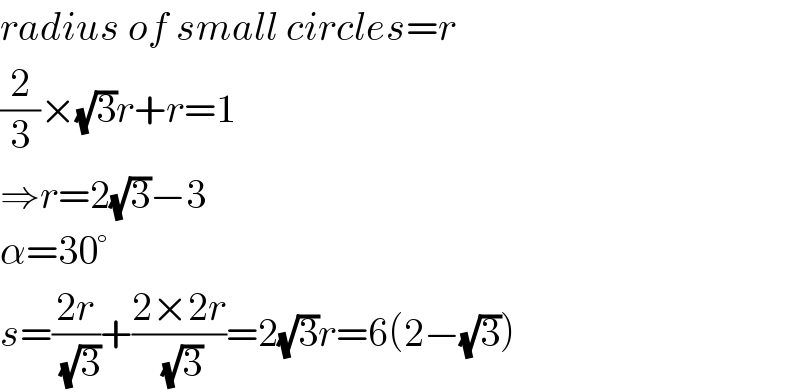
$${radius}\:{of}\:{small}\:{circles}={r} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}×\sqrt{\mathrm{3}}{r}+{r}=\mathrm{1} \\ $$$$\Rightarrow{r}=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3} \\ $$$$\alpha=\mathrm{30}° \\ $$$${s}=\frac{\mathrm{2}{r}}{\:\sqrt{\mathrm{3}}}+\frac{\mathrm{2}×\mathrm{2}{r}}{\:\sqrt{\mathrm{3}}}=\mathrm{2}\sqrt{\mathrm{3}}{r}=\mathrm{6}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$
Commented by ajfour last updated on 13/Jul/20
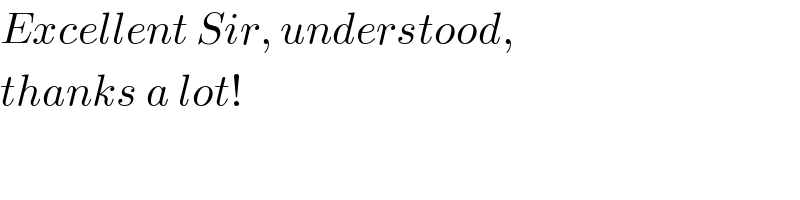
$${Excellent}\:{Sir},\:{understood}, \\ $$$${thanks}\:{a}\:{lot}! \\ $$
