Question Number 103171 by bemath last updated on 13/Jul/20

Commented by bobhans last updated on 13/Jul/20
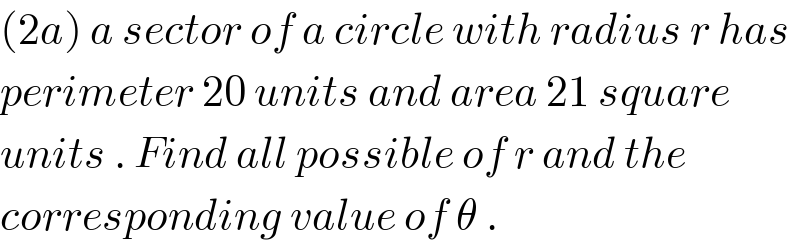
$$\left(\mathrm{2}{a}\right)\:{a}\:{sector}\:{of}\:{a}\:{circle}\:{with}\:{radius}\:{r}\:{has} \\ $$$${perimeter}\:\mathrm{20}\:{units}\:{and}\:{area}\:\mathrm{21}\:{square} \\ $$$${units}\:.\:{Find}\:{all}\:{possible}\:{of}\:{r}\:{and}\:{the}\: \\ $$$${corresponding}\:{value}\:{of}\:\theta\:. \\ $$
Answered by bobhans last updated on 13/Jul/20
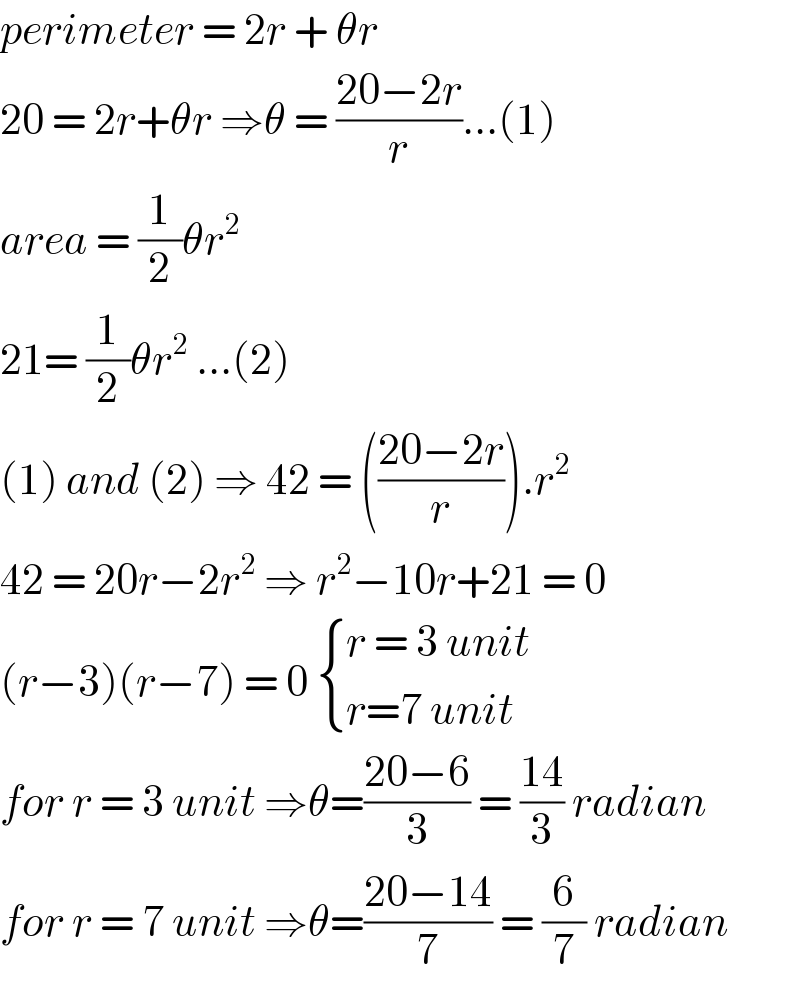
$${perimeter}\:=\:\mathrm{2}{r}\:+\:\theta{r}\: \\ $$$$\mathrm{20}\:=\:\mathrm{2}{r}+\theta{r}\:\Rightarrow\theta\:=\:\frac{\mathrm{20}−\mathrm{2}{r}}{{r}}…\left(\mathrm{1}\right) \\ $$$${area}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\theta{r}^{\mathrm{2}} \\ $$$$\mathrm{21}=\:\frac{\mathrm{1}}{\mathrm{2}}\theta{r}^{\mathrm{2}} \:…\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right)\:\Rightarrow\:\mathrm{42}\:=\:\left(\frac{\mathrm{20}−\mathrm{2}{r}}{{r}}\right).{r}^{\mathrm{2}} \\ $$$$\mathrm{42}\:=\:\mathrm{20}{r}−\mathrm{2}{r}^{\mathrm{2}} \:\Rightarrow\:{r}^{\mathrm{2}} −\mathrm{10}{r}+\mathrm{21}\:=\:\mathrm{0} \\ $$$$\left({r}−\mathrm{3}\right)\left({r}−\mathrm{7}\right)\:=\:\mathrm{0}\:\begin{cases}{{r}\:=\:\mathrm{3}\:{unit}}\\{{r}=\mathrm{7}\:{unit}}\end{cases} \\ $$$${for}\:{r}\:=\:\mathrm{3}\:{unit}\:\Rightarrow\theta=\frac{\mathrm{20}−\mathrm{6}}{\mathrm{3}}\:=\:\frac{\mathrm{14}}{\mathrm{3}}\:{radian} \\ $$$${for}\:{r}\:=\:\mathrm{7}\:{unit}\:\Rightarrow\theta=\frac{\mathrm{20}−\mathrm{14}}{\mathrm{7}}\:=\:\frac{\mathrm{6}}{\mathrm{7}}\:{radian} \\ $$
