Question Number 103179 by ajfour last updated on 13/Jul/20
Commented by ajfour last updated on 13/Jul/20
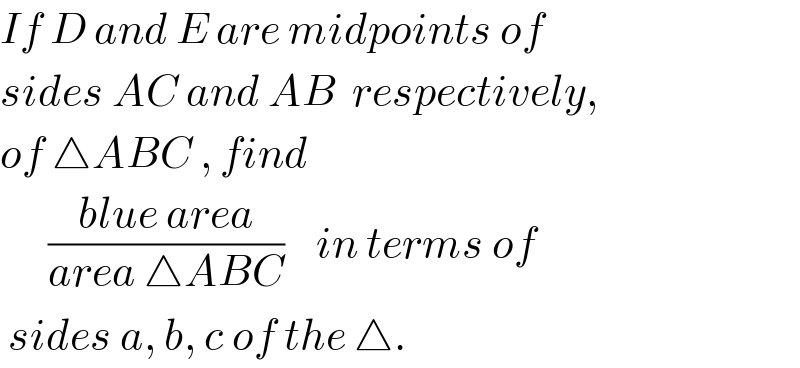
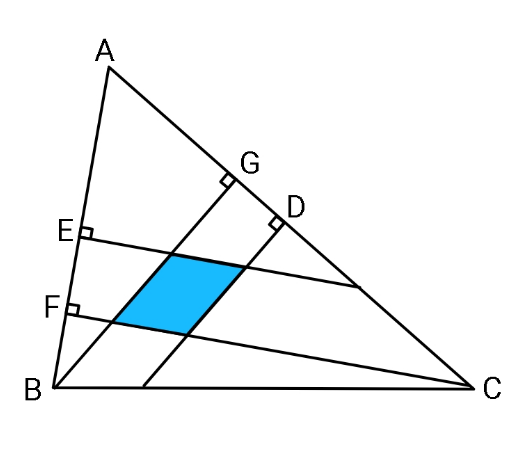
$${If}\:{D}\:{and}\:{E}\:{are}\:{midpoints}\:{of}\: \\ $$$${sides}\:{AC}\:{and}\:{AB}\:\:{respectively}, \\ $$$${of}\:\bigtriangleup{ABC}\:,\:{find}\: \\ $$$$\:\:\:\:\:\:\frac{{blue}\:{area}}{{area}\:\bigtriangleup{ABC}}\:\:\:\:{in}\:{terms}\:{of}\: \\ $$$$\:{sides}\:{a},\:{b},\:{c}\:{of}\:{the}\:\bigtriangleup. \\ $$
Answered by ajfour last updated on 13/Jul/20
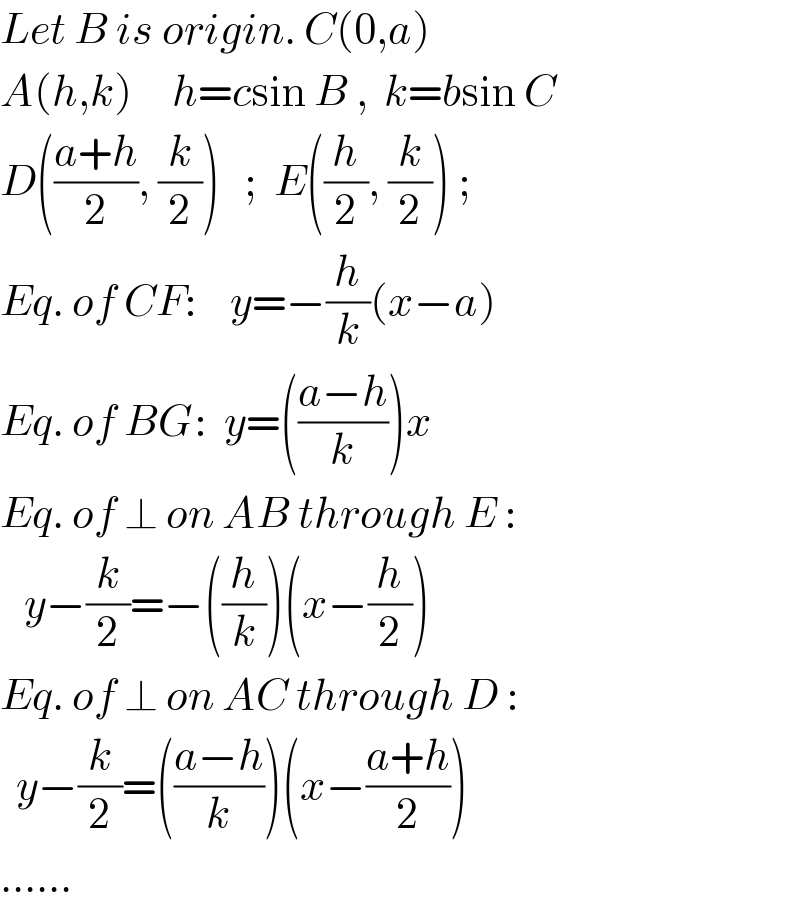
$${Let}\:{B}\:{is}\:{origin}.\:{C}\left(\mathrm{0},{a}\right) \\ $$$${A}\left({h},{k}\right)\:\:\:\:\:{h}={c}\mathrm{sin}\:{B}\:,\:\:{k}={b}\mathrm{sin}\:{C} \\ $$$${D}\left(\frac{{a}+{h}}{\mathrm{2}},\:\frac{{k}}{\mathrm{2}}\right)\:\:\:;\:\:{E}\left(\frac{{h}}{\mathrm{2}},\:\frac{{k}}{\mathrm{2}}\right)\:; \\ $$$${Eq}.\:{of}\:{CF}:\:\:\:\:{y}=−\frac{{h}}{{k}}\left({x}−{a}\right) \\ $$$${Eq}.\:{of}\:{BG}:\:\:{y}=\left(\frac{{a}−{h}}{{k}}\right){x} \\ $$$${Eq}.\:{of}\:\bot\:{on}\:{AB}\:{through}\:{E}\:: \\ $$$$\:\:\:{y}−\frac{{k}}{\mathrm{2}}=−\left(\frac{{h}}{{k}}\right)\left({x}−\frac{{h}}{\mathrm{2}}\right) \\ $$$${Eq}.\:{of}\:\bot\:{on}\:{AC}\:{through}\:{D}\:: \\ $$$$\:\:{y}−\frac{{k}}{\mathrm{2}}=\left(\frac{{a}−{h}}{{k}}\right)\left({x}−\frac{{a}+{h}}{\mathrm{2}}\right) \\ $$$$…… \\ $$
