Question Number 103228 by ajfour last updated on 13/Jul/20
Commented by ajfour last updated on 13/Jul/20
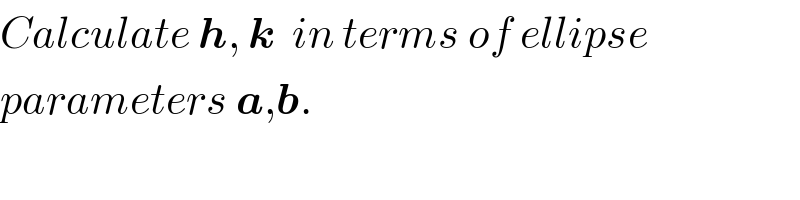
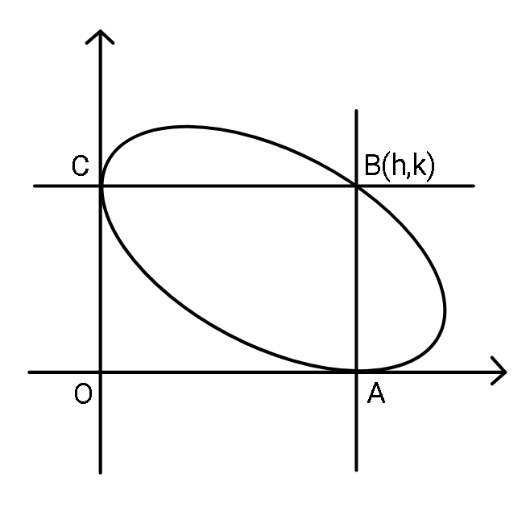
$${Calculate}\:\boldsymbol{{h}},\:\boldsymbol{{k}}\:\:{in}\:{terms}\:{of}\:{ellipse} \\ $$$${parameters}\:\boldsymbol{{a}},\boldsymbol{{b}}. \\ $$
Answered by mr W last updated on 13/Jul/20
Commented by mr W last updated on 15/Jul/20
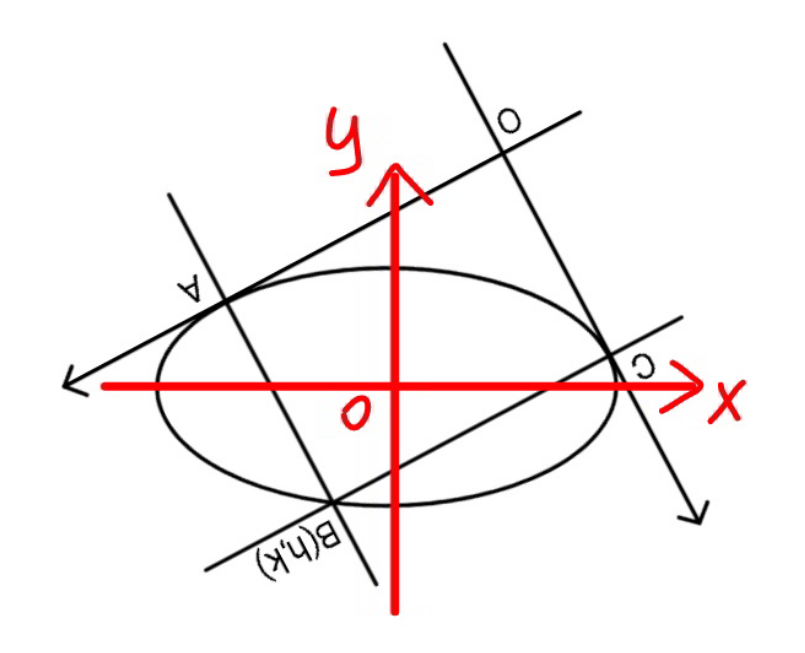
![let μ=(b/a) C(a cos θ, b sin θ) y′=−((b cos θ)/(a sin θ))=−(μ/(tan θ)) A(a cos ϕ, b sin ϕ) y′=−((b cos ϕ)/(a sin ϕ))=−(μ/(tan ϕ)) (−(μ/(tan ϕ)))(−(μ/(tan θ)))=−1 tan ϕ=−(μ^2 /(tan θ)) ⇒ϕ=π−tan^(−1) ((μ^2 /(tan θ))) eqn. of CB: y=((tan θ)/μ)(x−a cos θ)+b sin θ eqn. of AB: y=((tan ϕ)/μ)(x−a cos ϕ)+b sin ϕ ((tan ϕ)/μ)x_B +a(μ−(1/μ))sin ϕ=((tan θ)/μ)x_B +a(μ−(1/μ)) sin θ ⇒(x_B /a)=(((1−μ^2 )(sin θ−sin ϕ))/(tan θ−tan ϕ)) ⇒(y_B /b)=(((1−μ^2 )/μ^2 ))[(((sin θ−sin ϕ)tan θ)/(tan θ−tan ϕ))−sin θ] (x_B ^2 /a^2 )+(y_B ^2 /b^2 )=1 [((μ^2 (sin θ−sin ϕ))/(tan θ−tan ϕ))]^2 +[(((sin θ−sin ϕ)tan θ)/(tan θ−tan ϕ))−sin θ]^2 =((μ^2 /(1−μ^2 )))^2 ⇒ tan^2 θ(sin θ (√(μ^4 +tan^2 θ))−μ^2 )^2 +(sin θ (√(μ^4 +tan^2 θ))+tan^2 θ)^2 =(μ^4 +tan^2 θ)(((μ^2 +tan^2 θ)/(1−μ^2 )))^2 ⇒θ=... h=CB=(√((x_B −a cos θ)^2 +(y_B −b sin θ)^2 )) k=AB=(√((x_B −a cos ϕ)^2 +(y_B −b sin ϕ)^2 ))](https://www.tinkutara.com/question/Q103269.png)
$${let}\:\mu=\frac{{b}}{{a}} \\ $$$${C}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$${y}'=−\frac{{b}\:\mathrm{cos}\:\theta}{{a}\:\mathrm{sin}\:\theta}=−\frac{\mu}{\mathrm{tan}\:\theta} \\ $$$${A}\left({a}\:\mathrm{cos}\:\varphi,\:{b}\:\mathrm{sin}\:\varphi\right) \\ $$$${y}'=−\frac{{b}\:\mathrm{cos}\:\varphi}{{a}\:\mathrm{sin}\:\varphi}=−\frac{\mu}{\mathrm{tan}\:\varphi} \\ $$$$\left(−\frac{\mu}{\mathrm{tan}\:\varphi}\right)\left(−\frac{\mu}{\mathrm{tan}\:\theta}\right)=−\mathrm{1} \\ $$$$\mathrm{tan}\:\varphi=−\frac{\mu^{\mathrm{2}} }{\mathrm{tan}\:\theta} \\ $$$$\Rightarrow\varphi=\pi−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mu^{\mathrm{2}} }{\mathrm{tan}\:\theta}\right) \\ $$$${eqn}.\:{of}\:{CB}: \\ $$$${y}=\frac{\mathrm{tan}\:\theta}{\mu}\left({x}−{a}\:\mathrm{cos}\:\theta\right)+{b}\:\mathrm{sin}\:\theta \\ $$$${eqn}.\:{of}\:{AB}: \\ $$$${y}=\frac{\mathrm{tan}\:\varphi}{\mu}\left({x}−{a}\:\mathrm{cos}\:\varphi\right)+{b}\:\mathrm{sin}\:\varphi \\ $$$$\frac{\mathrm{tan}\:\varphi}{\mu}{x}_{{B}} +{a}\left(\mu−\frac{\mathrm{1}}{\mu}\right)\mathrm{sin}\:\varphi=\frac{\mathrm{tan}\:\theta}{\mu}{x}_{{B}} +{a}\left(\mu−\frac{\mathrm{1}}{\mu}\right)\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\frac{{x}_{{B}} }{{a}}=\frac{\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\left(\mathrm{sin}\:\theta−\mathrm{sin}\:\varphi\right)}{\mathrm{tan}\:\theta−\mathrm{tan}\:\varphi} \\ $$$$\Rightarrow\frac{{y}_{{B}} }{{b}}=\left(\frac{\mathrm{1}−\mu^{\mathrm{2}} }{\mu^{\mathrm{2}} }\right)\left[\frac{\left(\mathrm{sin}\:\theta−\mathrm{sin}\:\varphi\right)\mathrm{tan}\:\theta}{\mathrm{tan}\:\theta−\mathrm{tan}\:\varphi}−\mathrm{sin}\:\theta\right] \\ $$$$\frac{{x}_{{B}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}_{{B}} ^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\left[\frac{\mu^{\mathrm{2}} \left(\mathrm{sin}\:\theta−\mathrm{sin}\:\varphi\right)}{\mathrm{tan}\:\theta−\mathrm{tan}\:\varphi}\right]^{\mathrm{2}} +\left[\frac{\left(\mathrm{sin}\:\theta−\mathrm{sin}\:\varphi\right)\mathrm{tan}\:\theta}{\mathrm{tan}\:\theta−\mathrm{tan}\:\varphi}−\mathrm{sin}\:\theta\right]^{\mathrm{2}} =\left(\frac{\mu^{\mathrm{2}} }{\mathrm{1}−\mu^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{tan}^{\mathrm{2}} \:\theta\left(\mathrm{sin}\:\theta\:\sqrt{\mu^{\mathrm{4}} +\mathrm{tan}^{\mathrm{2}} \:\theta}−\mu^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:+\left(\mathrm{sin}\:\theta\:\sqrt{\mu^{\mathrm{4}} +\mathrm{tan}^{\mathrm{2}} \:\theta}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\left(\mu^{\mathrm{4}} +\mathrm{tan}^{\mathrm{2}} \:\theta\right)\left(\frac{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}{\mathrm{1}−\mu^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\Rightarrow\theta=… \\ $$$$ \\ $$$${h}={CB}=\sqrt{\left({x}_{{B}} −{a}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\left({y}_{{B}} −{b}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} } \\ $$$${k}={AB}=\sqrt{\left({x}_{{B}} −{a}\:\mathrm{cos}\:\varphi\right)^{\mathrm{2}} +\left({y}_{{B}} −{b}\:\mathrm{sin}\:\varphi\right)^{\mathrm{2}} } \\ $$
Commented by mr W last updated on 13/Jul/20
Commented by mr W last updated on 13/Jul/20
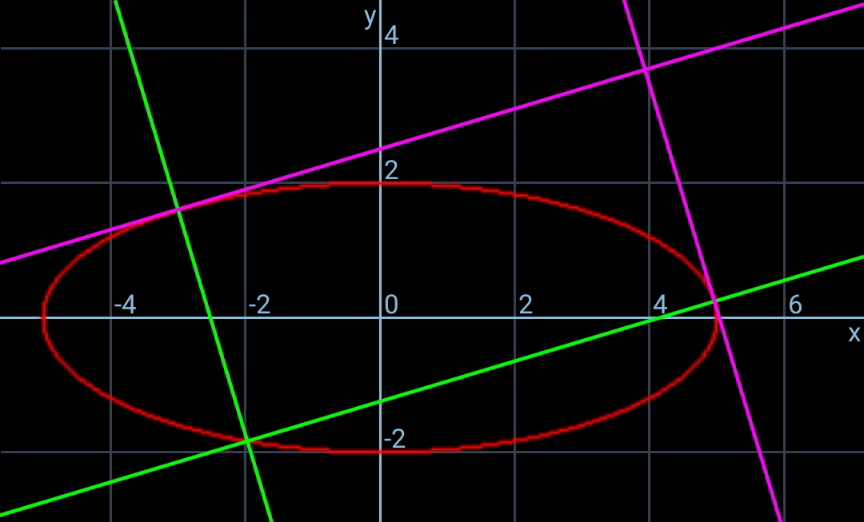
Commented by mr W last updated on 14/Jul/20
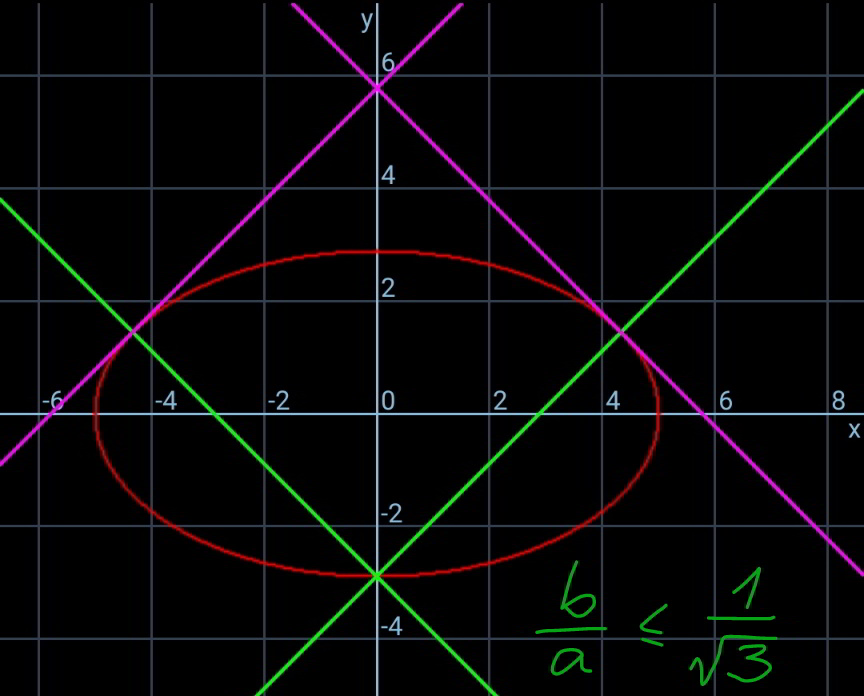
Commented by ajfour last updated on 17/Jul/20
![I have a nice way that results in quite a failure...please check n help! Let B(p,q) & inclination of BC is θ ⇒ inclination of AB is 90°+θ. BC = h, AB=k . B is on ellipse ⇒ b^2 p^2 +a^2 q^2 =a^2 b^2 _(−−−−−−−−−−−) ^(−−−−−−−−−−−) x_C = p+hcos θ ; y_C = q+hsin θ x_A = p−ksin θ ; y_A = q+kcos θ Ellipse eq: (x^2 /a^2 )+(y^2 /b^2 )=1 ⇒ slope of a normal at (x,y) is m = −(dx/dy)= ((a^2 /b^2 ))((y/x)) m_(BC) = tan θ = ((a^2 /b^2 ))(((q+hsin θ)/(p+hcos θ))) ..(i) m_(AB) =−(1/(tan θ))=((a^2 /b^2 ))(((q+kcos θ)/(p−ksin θ))) ..(ii) ⇒ (((b^2 p)/(cos θ))−((a^2 q)/(sin θ)))=(a^2 −b^2 )h ...(I) ⇒ −(((b^2 p)/(sin θ))+((a^2 q)/(cos θ)))=(a^2 −b^2 )k ...(II) Now C and A lie on ellipse ⇒ (x_C ^2 /a^2 )+(y_C ^2 /b^2 )=1 or b^2 (x_C )^2 +a^2 (y_C )^2 =a^2 b^2 ⇒b^2 (p+hcos θ)^2 +a^2 (q+hsin θ)^2 =a^2 b^2 and as b^2 p^2 +a^2 q^2 =a^2 b^2 so we have 2h(b^2 pcos θ+a^2 qsin θ) +h^2 (a^2 sin^2 θ+b^2 cos^2 θ) = 0 ⇒ −(((b^2 p)/(sin θ))+((a^2 q)/(sin θ)))=((h(a^2 sin^2 θ+b^2 cos^2 θ))/(2sin θcos θ)) Now using (II), (a^2 −b^2 )k=((h(a^2 sin^2 θ+b^2 cos^2 θ))/(2sin θcos θ)) ...(iii) (x_A ^2 /a^2 )+(y_A ^2 /b^2 )=1 ⇒ b^2 (x_A )^2 +a^2 (y_A )^2 =a^2 b^2 ⇒ b^2 (p−ksin θ)^2 +a^2 (q+kcos θ)^2 =a^2 b^2 and as b^2 p^2 +a^2 q^2 =a^2 b^2 so we have 2k(−b^2 psin θ+a^2 qcos θ) +k^2 (b^2 sin^2 θ+a^2 cos^2 θ) = 0 ⇒ ((b^2 p)/(cos θ))−((a^2 q)/(sin θ)) = ((k(b^2 sin^2 θ+a^2 cos^2 θ))/(2sin θcos θ)) Now using (I), (a^2 −b^2 )h=((k(b^2 sin^2 θ+a^2 cos^2 θ))/(2sin θcos θ)) ...(iv) and already we have (a^2 −b^2 )k=((h(a^2 sin^2 θ+b^2 cos^2 θ))/(2sin θcos θ)) ...(iii) Now (iii)×(iv) with m=tan θ gives 4(a^2 −b^2 )^2 m^2 =(b^2 m^2 +a^2 )(a^2 m^2 +b^3 ) ⇒ m^4 +{((a^4 +b^4 −4(a^2 −b^2 )^2 )/(a^2 b^2 ))}m^2 +1=0 let a/b = μ ⇒ m^4 +{μ^2 +(1/μ^2 )−4(μ−(1/μ))^2 }m^2 +1=0 {m^2 +1−(3/2)(μ−(1/μ))^2 }^2 = [1−(3/2)(μ−(1/μ))^2 ]^2 −1 Now tragedy is unless 𝛍=1 , m^2 ∉R so mrW Sir kindly help me out of this turmoil .... If m=tan θ, were real h and k could easily be obtained...](https://www.tinkutara.com/question/Q103707.png)
$${I}\:{have}\:{a}\:{nice}\:{way}\:{that}\:{results}\:{in}\: \\ $$$${quite}\:{a}\:{failure}…{please}\:{check}\:{n}\:{help}! \\ $$$${Let} \\ $$$$\:\:\:{B}\left({p},{q}\right)\:\:\:\&\:{inclination}\:{of}\:{BC}\:\:{is}\:\:\theta \\ $$$$\Rightarrow\:{inclination}\:{of}\:{AB}\:\:{is}\:\mathrm{90}°+\theta. \\ $$$$\:\:\:{BC}\:=\:{h},\:\:{AB}={k}\:. \\ $$$${B}\:{is}\:{on}\:{ellipse}\:\Rightarrow\:\underset{−−−−−−−−−−−} {\:{b}^{\mathrm{2}} {p}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \:} \\ $$$$\:\:\:\:\:\:{x}_{{C}} =\:{p}+{h}\mathrm{cos}\:\theta\:;\:\:{y}_{{C}} =\:{q}+{h}\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:{x}_{{A}} =\:{p}−{k}\mathrm{sin}\:\theta\:;\:\:{y}_{{A}} =\:{q}+{k}\mathrm{cos}\:\theta \\ $$$$\:\:{Ellipse}\:\:{eq}:\:\:\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\:\:\:\:\:\:\Rightarrow\:\:\:{slope}\:{of}\:{a}\:{normal}\:{at}\:\left({x},{y}\right)\:{is} \\ $$$$\:\:\:\:\:{m}\:=\:−\frac{{dx}}{{dy}}=\:\left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)\left(\frac{{y}}{{x}}\right) \\ $$$$\:\:\:{m}_{{BC}} =\:\mathrm{tan}\:\theta\:=\:\left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)\left(\frac{{q}+{h}\mathrm{sin}\:\theta}{{p}+{h}\mathrm{cos}\:\theta}\right)\:..\left({i}\right) \\ $$$$\:\:\:{m}_{{AB}} =−\frac{\mathrm{1}}{\mathrm{tan}\:\theta}=\left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)\left(\frac{{q}+{k}\mathrm{cos}\:\theta}{{p}−{k}\mathrm{sin}\:\theta}\right)\:..\left({ii}\right) \\ $$$$\Rightarrow\:\:\left(\frac{{b}^{\mathrm{2}} {p}}{\mathrm{cos}\:\theta}−\frac{{a}^{\mathrm{2}} {q}}{\mathrm{sin}\:\theta}\right)=\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){h}\:\:\:\:…\left({I}\right) \\ $$$$\Rightarrow\:\:−\left(\frac{{b}^{\mathrm{2}} {p}}{\mathrm{sin}\:\theta}+\frac{{a}^{\mathrm{2}} {q}}{\mathrm{cos}\:\theta}\right)=\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){k}\:\:\:…\left({II}\right) \\ $$$${Now}\:{C}\:{and}\:{A}\:{lie}\:{on}\:{ellipse}\:\Rightarrow \\ $$$$\:\:\frac{{x}_{{C}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}_{{C}} ^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:{or}\:\:\:{b}^{\mathrm{2}} \left({x}_{{C}} \right)^{\mathrm{2}} +{a}^{\mathrm{2}} \left({y}_{{C}} \right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\Rightarrow{b}^{\mathrm{2}} \left({p}+{h}\mathrm{cos}\:\theta\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \left({q}+{h}\mathrm{sin}\:\theta\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$${and}\:{as}\:\:\:{b}^{\mathrm{2}} {p}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \:\:\:{so}\:{we}\:{have} \\ $$$$\:\:\mathrm{2}{h}\left({b}^{\mathrm{2}} {p}\mathrm{cos}\:\theta+{a}^{\mathrm{2}} {q}\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:+{h}^{\mathrm{2}} \left({a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:−\left(\frac{{b}^{\mathrm{2}} {p}}{\mathrm{sin}\:\theta}+\frac{{a}^{\mathrm{2}} {q}}{\mathrm{sin}\:\theta}\right)=\frac{{h}\left({a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right)}{\mathrm{2sin}\:\theta\mathrm{cos}\:\theta} \\ $$$${Now}\:\:{using}\:\left({II}\right), \\ $$$$\:\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){k}=\frac{{h}\left({a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right)}{\mathrm{2sin}\:\theta\mathrm{cos}\:\theta}\:\:…\left({iii}\right) \\ $$$$\frac{{x}_{{A}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}_{{A}} ^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\Rightarrow\:\:{b}^{\mathrm{2}} \left({x}_{{A}} \right)^{\mathrm{2}} +{a}^{\mathrm{2}} \left({y}_{{A}} \right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\: \\ $$$$\:{b}^{\mathrm{2}} \left({p}−{k}\mathrm{sin}\:\theta\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \left({q}+{k}\mathrm{cos}\:\theta\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$${and}\:{as}\:\:\:{b}^{\mathrm{2}} {p}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \:\:\:{so}\:{we}\:{have} \\ $$$$\:\mathrm{2}{k}\left(−{b}^{\mathrm{2}} {p}\mathrm{sin}\:\theta+{a}^{\mathrm{2}} {q}\mathrm{cos}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:+{k}^{\mathrm{2}} \left({b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\frac{{b}^{\mathrm{2}} {p}}{\mathrm{cos}\:\theta}−\frac{{a}^{\mathrm{2}} {q}}{\mathrm{sin}\:\theta}\:=\:\frac{{k}\left({b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right)}{\mathrm{2sin}\:\theta\mathrm{cos}\:\theta} \\ $$$${Now}\:\:{using}\:\left({I}\right), \\ $$$$\:\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){h}=\frac{{k}\left({b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right)}{\mathrm{2sin}\:\theta\mathrm{cos}\:\theta}\:\:…\left({iv}\right) \\ $$$${and}\:\:{already}\:{we}\:{have}\: \\ $$$$\:\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){k}=\frac{{h}\left({a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right)}{\mathrm{2sin}\:\theta\mathrm{cos}\:\theta}\:\:…\left({iii}\right) \\ $$$${Now}\:\:\:\left({iii}\right)×\left({iv}\right)\:\:{with}\:\:{m}=\mathrm{tan}\:\theta\:{gives} \\ $$$$\mathrm{4}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} {m}^{\mathrm{2}} =\left({b}^{\mathrm{2}} {m}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{3}} \right) \\ $$$$\Rightarrow\:\:{m}^{\mathrm{4}} +\left\{\frac{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} −\mathrm{4}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\right\}{m}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\:\:{let}\:\:{a}/{b}\:=\:\mu \\ $$$$\Rightarrow\:\:{m}^{\mathrm{4}} +\left\{\mu^{\mathrm{2}} +\frac{\mathrm{1}}{\mu^{\mathrm{2}} }−\mathrm{4}\left(\mu−\frac{\mathrm{1}}{\mu}\right)^{\mathrm{2}} \right\}{m}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\left\{{m}^{\mathrm{2}} +\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}\left(\mu−\frac{\mathrm{1}}{\mu}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\:\left[\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}\left(\mu−\frac{\mathrm{1}}{\mu}\right)^{\mathrm{2}} \right]^{\mathrm{2}} −\mathrm{1} \\ $$$${Now}\:\:{tragedy}\:{is}\:{unless}\:\boldsymbol{\mu}=\mathrm{1}\:,\:{m}^{\mathrm{2}} \notin\mathbb{R}\: \\ $$$$\:\:\:\:\:{so}\:\:{mrW}\:{Sir}\:\:{kindly}\:{help}\:{me} \\ $$$${out}\:\:{of}\:{this}\:{turmoil}\:…. \\ $$$${If}\:\:{m}=\mathrm{tan}\:\theta,\:\:{were}\:{real}\:{h}\:{and}\:{k}\:{could} \\ $$$${easily}\:{be}\:{obtained}… \\ $$$$\: \\ $$
Commented by ajfour last updated on 16/Jul/20

$${thanks}\:{sir},\:{some}\:{consolation}\:{at} \\ $$$${least};\:{but}\:{there}\:{must}\:{be},\:{or}\:{you} \\ $$$${couldn}'{t}\:{have}\:{graphed}\:{your}\:{solution}.. \\ $$
Commented by mr W last updated on 16/Jul/20

$${perfect}\:{solution}! \\ $$
Commented by mr W last updated on 17/Jul/20
![i think all correct! ⇒ m^4 +{μ^2 +(1/μ^2 )−4(μ−(1/μ))^2 }m^2 +1=0 ⇒ m^4 +[2−3(μ−(1/μ))^2 ]m^2 +1=0 ⇒two roots for m^2 for μ≥(√3). for μ=(√3) there should be one single root θ=45°, i.e. m=1. 1^4 +[2−3((√3)−(1/( (√3))))^2 ]1^2 +1=0 ⇒true!](https://www.tinkutara.com/question/Q103726.png)
$${i}\:{think}\:{all}\:{correct}! \\ $$$$\Rightarrow\:\:{m}^{\mathrm{4}} +\left\{\mu^{\mathrm{2}} +\frac{\mathrm{1}}{\mu^{\mathrm{2}} }−\mathrm{4}\left(\mu−\frac{\mathrm{1}}{\mu}\right)^{\mathrm{2}} \right\}{m}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:{m}^{\mathrm{4}} +\left[\mathrm{2}−\mathrm{3}\left(\mu−\frac{\mathrm{1}}{\mu}\right)^{\mathrm{2}} \right]{m}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{two}\:{roots}\:{for}\:{m}^{\mathrm{2}} \:{for}\:\mu\geqslant\sqrt{\mathrm{3}}. \\ $$$${for}\:\mu=\sqrt{\mathrm{3}}\:{there}\:{should}\:{be}\:{one}\:{single} \\ $$$${root}\:\theta=\mathrm{45}°,\:{i}.{e}.\:{m}=\mathrm{1}. \\ $$$$\mathrm{1}^{\mathrm{4}} +\left[\mathrm{2}−\mathrm{3}\left(\sqrt{\mathrm{3}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} \right]\mathrm{1}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\:\Rightarrow{true}! \\ $$
Commented by ajfour last updated on 17/Jul/20
$${Thanks}\:{enormously}\:{Sir}!\:\left({edited}\right) \\ $$
