Question Number 103366 by Study last updated on 14/Jul/20

Answered by mathmax by abdo last updated on 14/Jul/20

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{4}}} −\mathrm{5}^{\frac{\mathrm{1}}{\left\{\right.}} }{\left(\mathrm{lnx}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} −\left(\mathrm{ln5}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} }\:\:\mathrm{let}\:\mathrm{find}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{5}} \mathrm{f}\left(\mathrm{x}\right)\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement} \\ $$$$\mathrm{x}\:=\mathrm{5}−\mathrm{t}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{g}\left(\mathrm{t}\right)\:=\frac{\left(\mathrm{5}−\mathrm{t}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} −\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} }{\left(\mathrm{ln}\left(\mathrm{5}−\mathrm{t}\right)\right)^{\frac{\mathrm{1}}{\mathrm{8}}} −\left(\mathrm{ln5}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} }\:\:\:\left(\mathrm{t}\rightarrow\mathrm{0}\right) \\ $$$$=\frac{\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} \left\{\left(\mathrm{1}−\frac{\mathrm{t}}{\mathrm{5}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} −\mathrm{1}\right\}}{\left(\mathrm{ln}\left(\mathrm{5}\right)+\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{t}}{\mathrm{5}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{8}}} −\left(\mathrm{ln5}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} } \\ $$$$\Rightarrow\mathrm{g}\left(\mathrm{t}\right)\:\sim\frac{\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} \left\{\mathrm{1}−\frac{\mathrm{t}}{\mathrm{20}}−\mathrm{1}\right\}}{\left(\mathrm{ln}\left(\mathrm{5}\right)−\frac{\mathrm{t}}{\mathrm{5}}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} −\left(\mathrm{ln5}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} }\:=\frac{\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} \left\{−\frac{\mathrm{t}}{\mathrm{20}}\right\}}{\left(\mathrm{ln5}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} \left\{\left(\mathrm{1}−\frac{\mathrm{t}}{\mathrm{5ln5}}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} −\mathrm{1}\right\}} \\ $$$$\sim\frac{\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} \left\{−\frac{\mathrm{t}}{\mathrm{20}}\right\}}{\left(\mathrm{ln5}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} \left\{\mathrm{1}−\frac{\mathrm{t}}{\mathrm{40ln5}}−\mathrm{1}\right\}}\:\rightarrow\frac{\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} }{\left(\mathrm{ln5}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} }×\frac{\mathrm{40ln5}}{\mathrm{20}}\:=\frac{\mathrm{2}\:\mathrm{ln5}\:×\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} }{\left(\mathrm{ln5}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} } \\ $$$$=\mathrm{2}.\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} \:\left(\mathrm{ln5}\right)^{\frac{\mathrm{7}}{\mathrm{8}}} \:\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{5}} \mathrm{f}\left(\mathrm{x}\right)=\:\mathrm{2}\left(^{\mathrm{4}} \sqrt{\mathrm{5}}\right)\left(\mathrm{ln5}\right)^{\frac{\mathrm{7}}{\mathrm{8}}} \\ $$
Answered by bemath last updated on 14/Jul/20

$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{5}} {\mathrm{lim}}\:\:\frac{\sqrt[{\mathrm{4}}]{{x}}−\sqrt[{\mathrm{4}}]{\mathrm{5}}}{\:\sqrt[{\mathrm{8}}]{\mathrm{ln}{x}}\:−\sqrt[{\mathrm{8}}]{\mathrm{ln}\:\mathrm{5}}}\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{5}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{4}\:{x}^{\mathrm{3}/\mathrm{4}} }}{\frac{\mathrm{1}}{\mathrm{8}{x}\:\left(\mathrm{ln}\:{x}\right)^{\mathrm{7}/\mathrm{8}} }}\:=\:\underset{{x}\rightarrow\mathrm{5}} {\mathrm{lim}}\:\frac{\mathrm{8}{x}\:\left(\mathrm{ln}\:{x}\right)^{\mathrm{7}/\mathrm{8}} }{\mathrm{4}{x}^{\mathrm{3}/\mathrm{4}} } \\ $$$$=\:\frac{\mathrm{10}.\left(\mathrm{ln}\:\mathrm{5}\right)^{\mathrm{7}/\mathrm{8}} }{\mathrm{5}^{\mathrm{3}/\mathrm{4}} }\:\blacksquare\: \\ $$
Answered by bemath last updated on 14/Jul/20
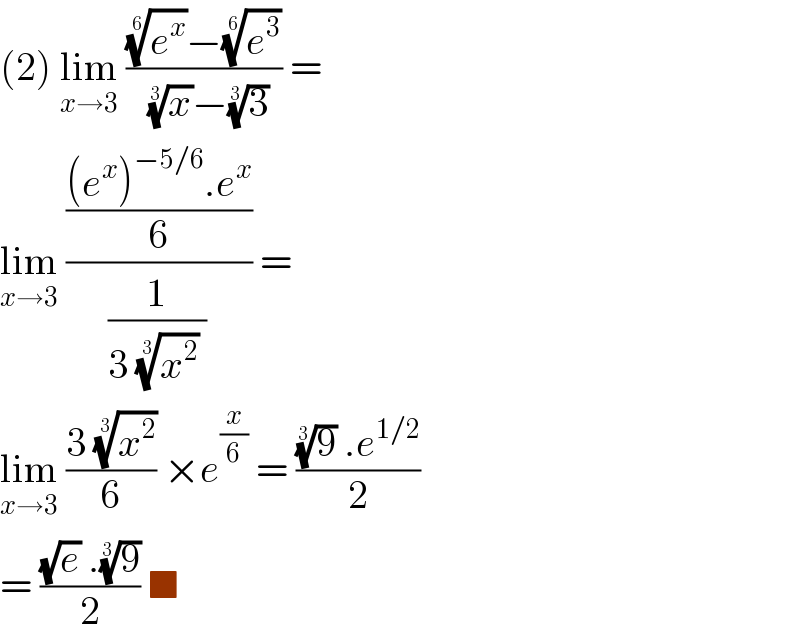
$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{6}}]{{e}^{{x}} }−\sqrt[{\mathrm{6}}]{{e}^{\mathrm{3}} }}{\:\sqrt[{\mathrm{3}}]{{x}}−\sqrt[{\mathrm{3}}]{\mathrm{3}}}\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\frac{\left({e}^{{x}} \right)^{−\mathrm{5}/\mathrm{6}} .{e}^{{x}} }{\mathrm{6}}}{\frac{\mathrm{1}}{\mathrm{3}\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} }\:}}\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\mathrm{3}\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} }}{\mathrm{6}}\:×{e}^{\frac{{x}}{\mathrm{6}}} \:=\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{9}}\:.{e}^{\mathrm{1}/\mathrm{2}} }{\mathrm{2}}\: \\ $$$$=\:\frac{\sqrt{{e}}\:.\sqrt[{\mathrm{3}}]{\mathrm{9}}}{\mathrm{2}}\:\blacksquare \\ $$
Answered by mathmax by abdo last updated on 15/Jul/20

$$\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{6}}} −\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{cha7gement}\:\mathrm{t}\:=\mathrm{x}−\mathrm{3}\:\left(\mathrm{so}\:\mathrm{t}\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{e}^{\frac{\mathrm{t}+\mathrm{3}}{\mathrm{6}}} −\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{t}+\mathrm{3}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:=\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}} \left\{\mathrm{e}^{\frac{\mathrm{t}}{\mathrm{6}}} −\mathrm{1}\right\}}{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} \left\{\:\left(\mathrm{1}+\frac{\mathrm{t}}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{1}\right\}}\:=\varphi\left(\mathrm{t}\right)\:\Rightarrow \\ $$$$\varphi\left(\mathrm{t}\right)\:\sim\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} }\left\{\:\frac{\mathrm{1}+\frac{\mathrm{t}}{\mathrm{6}}−\mathrm{1}}{\mathrm{1}+\frac{\mathrm{t}}{\mathrm{9}}−\mathrm{1}}\right\}\:\rightarrow\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} }×\frac{\mathrm{9}}{\mathrm{6}}\:=\frac{\mathrm{3}}{\mathrm{2}}×\frac{\sqrt{\mathrm{e}}}{\left(^{\mathrm{3}} \sqrt{\mathrm{3}}\right)}\left(\mathrm{t}\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{lim}\:_{\mathrm{x}\rightarrow\mathrm{3}} \mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{3}\sqrt{\mathrm{e}}}{\mathrm{2}\left(^{\mathrm{3}} \sqrt{\mathrm{3}}\right)} \\ $$
