Question Number 103389 by M±th+et+s last updated on 14/Jul/20

Commented by M±th+et+s last updated on 14/Jul/20
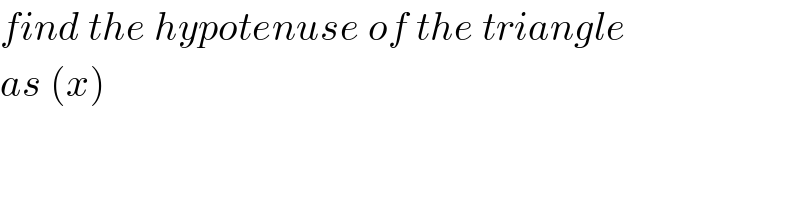
$${find}\:{the}\:{hypotenuse}\:{of}\:{the}\:{triangle} \\ $$$${as}\:\left({x}\right) \\ $$
Answered by OlafThorendsen last updated on 14/Jul/20
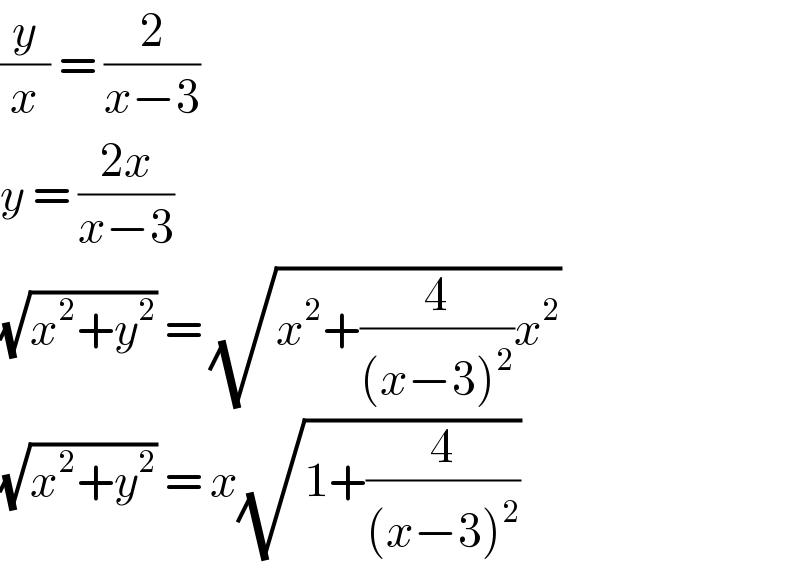
$$\frac{{y}}{{x}}\:=\:\frac{\mathrm{2}}{{x}−\mathrm{3}} \\ $$$${y}\:=\:\frac{\mathrm{2}{x}}{{x}−\mathrm{3}} \\ $$$$\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\:\sqrt{{x}^{\mathrm{2}} +\frac{\mathrm{4}}{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }{x}^{\mathrm{2}} } \\ $$$$\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\:{x}\sqrt{\mathrm{1}+\frac{\mathrm{4}}{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }} \\ $$
Answered by bramlex last updated on 15/Jul/20

Commented by bramlex last updated on 15/Jul/20

$$\frac{\mathrm{x}−\mathrm{3}}{\mathrm{3}}\:=\:\frac{\mathrm{2}}{\mathrm{y}−\mathrm{2}}\:\Rightarrow\frac{\mathrm{y}−\mathrm{2}}{\mathrm{2}}\:=\:\frac{\mathrm{3}}{\mathrm{x}−\mathrm{3}} \\ $$$$\mathrm{y}\:=\:\frac{\mathrm{6}}{\mathrm{x}−\mathrm{3}}\:+\:\mathrm{2}\:=\:\frac{\mathrm{6}+\mathrm{2x}−\mathrm{6}}{\mathrm{x}−\mathrm{3}} \\ $$$$\mathrm{y}=\:\frac{\mathrm{2x}}{\mathrm{x}−\mathrm{3}}.\: \\ $$$$\mathrm{hypotenusa}\:\mathrm{r}\:=\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} } \\ $$$$\mathrm{r}\:=\:\sqrt{\mathrm{x}^{\mathrm{2}} +\left(\frac{\mathrm{2x}}{\mathrm{x}−\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{r}=\:\sqrt{\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} +\mathrm{4x}^{\mathrm{2}} }{\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} }} \\ $$$$\mathrm{r}\:=\:\frac{\mathrm{x}}{\mathrm{x}−\mathrm{3}}.\sqrt{\mathrm{4}+\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{9}} \\ $$$$\mathrm{r}\:=\:\frac{\mathrm{x}}{\mathrm{x}−\mathrm{3}}.\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{6}+\mathrm{13}}\:\blacksquare \\ $$
