Question Number 103449 by aurpeyz last updated on 15/Jul/20

Answered by Worm_Tail last updated on 15/Jul/20
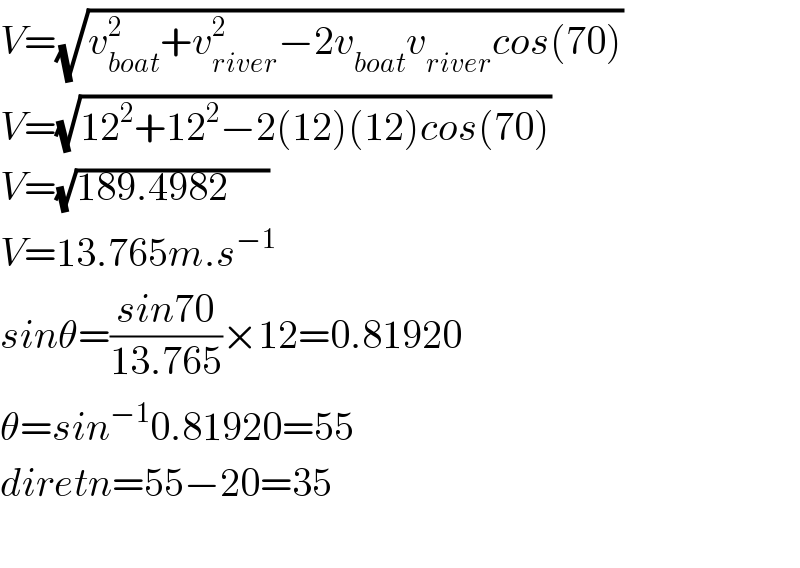
$${V}=\sqrt{{v}_{{boat}} ^{\mathrm{2}} +{v}_{{river}} ^{\mathrm{2}} −\mathrm{2}{v}_{{boat}} {v}_{{river}} {cos}\left(\mathrm{70}\right)} \\ $$$${V}=\sqrt{\mathrm{12}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{12}\right)\left(\mathrm{12}\right){cos}\left(\mathrm{70}\right)} \\ $$$${V}=\sqrt{\mathrm{189}.\mathrm{4982}\:\:\:\:\:} \\ $$$${V}=\mathrm{13}.\mathrm{765}{m}.{s}^{−\mathrm{1}} \\ $$$${sin}\theta=\frac{{sin}\mathrm{70}}{\mathrm{13}.\mathrm{765}}×\mathrm{12}=\mathrm{0}.\mathrm{81920} \\ $$$$\theta={sin}^{−\mathrm{1}} \mathrm{0}.\mathrm{81920}=\mathrm{55} \\ $$$${diretn}=\mathrm{55}−\mathrm{20}=\mathrm{35} \\ $$$$ \\ $$
Commented by aurpeyz last updated on 15/Jul/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
