Question Number 103510 by 175mohamed last updated on 15/Jul/20

Commented by Worm_Tail last updated on 15/Jul/20

$${y}={cot}^{−\mathrm{1}} \left({x}\right)\Rightarrow{cot}\left({y}\right)={x} \\ $$$${tan}\left({y}\right)=\frac{\mathrm{1}}{{x}}\Rightarrow{y}={tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}} \\ $$$${cot}^{−\mathrm{1}} {x}={tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}} \\ $$$$ \\ $$$${my}\:\:\:{plot}\:\:\:{down}\:\:\:\:{the}\:\:{comment}\:\:{from}\:\:\:{geogebra} \\ $$$$ \\ $$
Commented by Worm_Tail last updated on 15/Jul/20

Commented by PRITHWISH SEN 2 last updated on 15/Jul/20

$$\because\:\mathrm{both}\:\mathrm{are}\:\mathrm{periodic}\:\mathrm{functions}\:\mathrm{but}\:\mathrm{the}\:\mathrm{both}\:\mathrm{do}\:\mathrm{not} \\ $$$$\mathrm{have}\:\mathrm{the}\:\mathrm{same}\:\mathrm{period}\:\mathrm{of}\:\mathrm{interval}. \\ $$$$\mathrm{the}\:\mathrm{inverse}\:\mathrm{of}\:\mathrm{tan}\:\mathrm{will}\:\mathrm{be}\:\mathrm{in}\:\mathrm{the}\:\mathrm{domain}\:\mathrm{of}\: \\ $$$$−\frac{\pi}{\mathrm{2}}\:\mathrm{to}\:\frac{\pi}{\mathrm{2}}\:\mathrm{and}\:\mathrm{for}\:\mathrm{the}\:\mathrm{cot}\:\mathrm{it}\:\mathrm{is}\:\mathrm{from}\:\mathrm{0}\:\mathrm{to}\:\pi \\ $$$$\therefore\:\mathrm{you}\:\mathrm{can}'\mathrm{t}\:\mathrm{replace}\:\mathrm{cot}^{−\mathrm{1}} \:\mathrm{by}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{0}\:\mathrm{to}\:−\infty\:\mathrm{domain}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 15/Jul/20
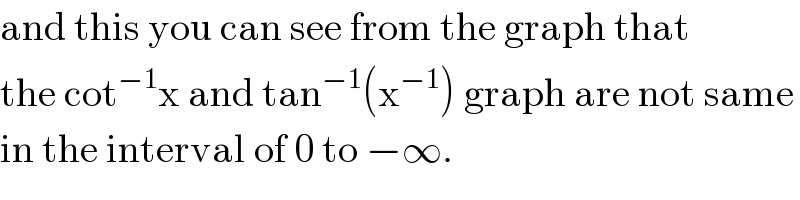
$$\mathrm{and}\:\mathrm{this}\:\mathrm{you}\:\mathrm{can}\:\mathrm{see}\:\mathrm{from}\:\mathrm{the}\:\mathrm{graph}\:\mathrm{that}\: \\ $$$$\mathrm{the}\:\mathrm{cot}^{−\mathrm{1}} \mathrm{x}\:\mathrm{and}\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}^{−\mathrm{1}} \right)\:\mathrm{graph}\:\mathrm{are}\:\mathrm{not}\:\mathrm{same} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{interval}\:\mathrm{of}\:\mathrm{0}\:\mathrm{to}\:−\infty. \\ $$
Commented by abdomathmax last updated on 16/Jul/20
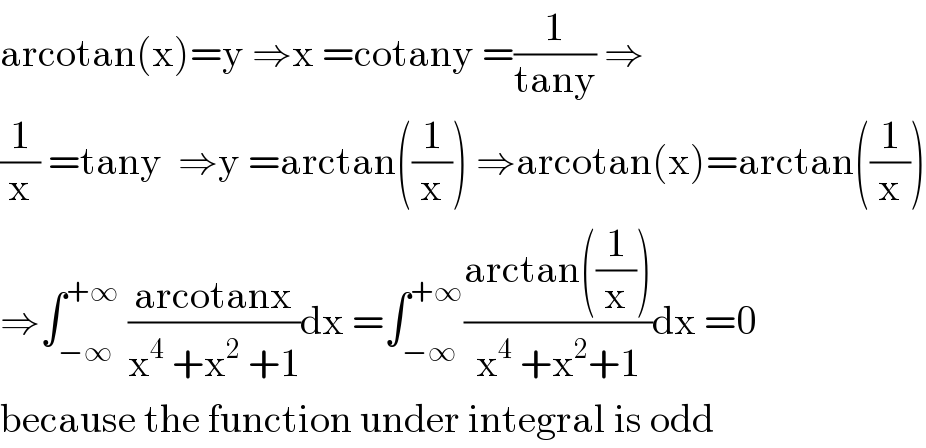
$$\mathrm{arcotan}\left(\mathrm{x}\right)=\mathrm{y}\:\Rightarrow\mathrm{x}\:=\mathrm{cotany}\:=\frac{\mathrm{1}}{\mathrm{tany}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}\:=\mathrm{tany}\:\:\Rightarrow\mathrm{y}\:=\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:\Rightarrow\mathrm{arcotan}\left(\mathrm{x}\right)=\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$\Rightarrow\int_{−\infty} ^{+\infty} \:\frac{\mathrm{arcotanx}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\int_{−\infty} ^{+\infty} \frac{\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:=\mathrm{0} \\ $$$$\mathrm{because}\:\mathrm{the}\:\mathrm{function}\:\mathrm{under}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{odd} \\ $$
Answered by Worm_Tail last updated on 15/Jul/20
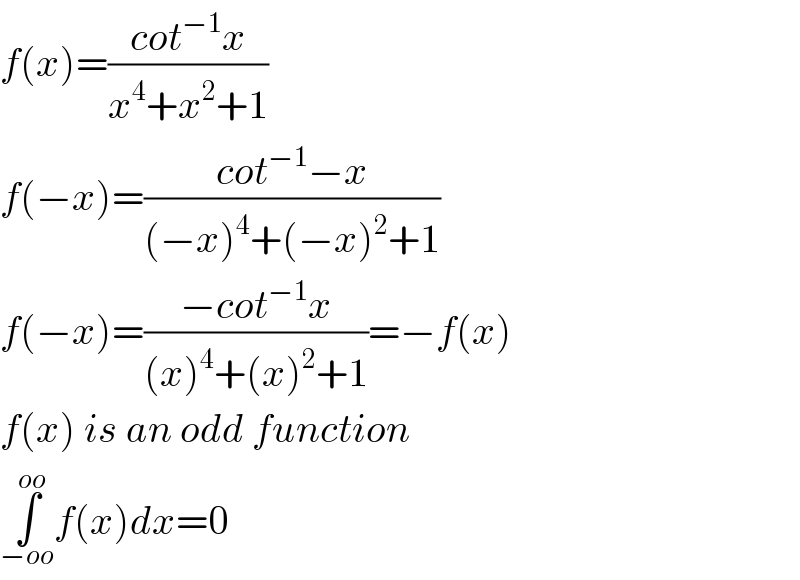
$${f}\left({x}\right)=\frac{{cot}^{−\mathrm{1}} {x}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${f}\left(−{x}\right)=\frac{{cot}^{−\mathrm{1}} −{x}}{\left(−{x}\right)^{\mathrm{4}} +\left(−{x}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$${f}\left(−{x}\right)=\frac{−{cot}^{−\mathrm{1}} {x}}{\left({x}\right)^{\mathrm{4}} +\left({x}\right)^{\mathrm{2}} +\mathrm{1}}=−{f}\left({x}\right) \\ $$$${f}\left({x}\right)\:{is}\:{an}\:{odd}\:{function} \\ $$$$\underset{−{oo}} {\overset{{oo}} {\int}}{f}\left({x}\right){dx}=\mathrm{0} \\ $$
Commented by PRITHWISH SEN 2 last updated on 15/Jul/20

Commented by PRITHWISH SEN 2 last updated on 15/Jul/20

$$\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{function} \\ $$
Commented by PRITHWISH SEN 2 last updated on 15/Jul/20
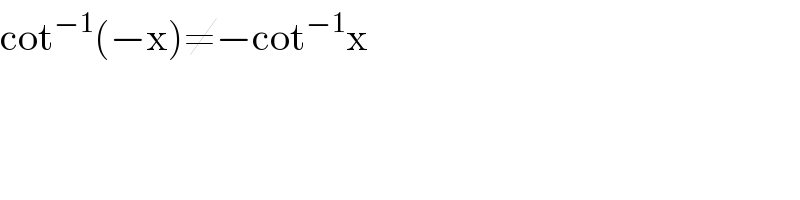
$$\mathrm{cot}^{−\mathrm{1}} \left(−\mathrm{x}\right)\neq−\mathrm{cot}^{−\mathrm{1}} \mathrm{x} \\ $$
Commented by PRITHWISH SEN 2 last updated on 15/Jul/20

Commented by Worm_Tail last updated on 15/Jul/20

