Question-103553

Question Number 103553 by byaw last updated on 15/Jul/20

Answered by mathmax by abdo last updated on 16/Jul/20

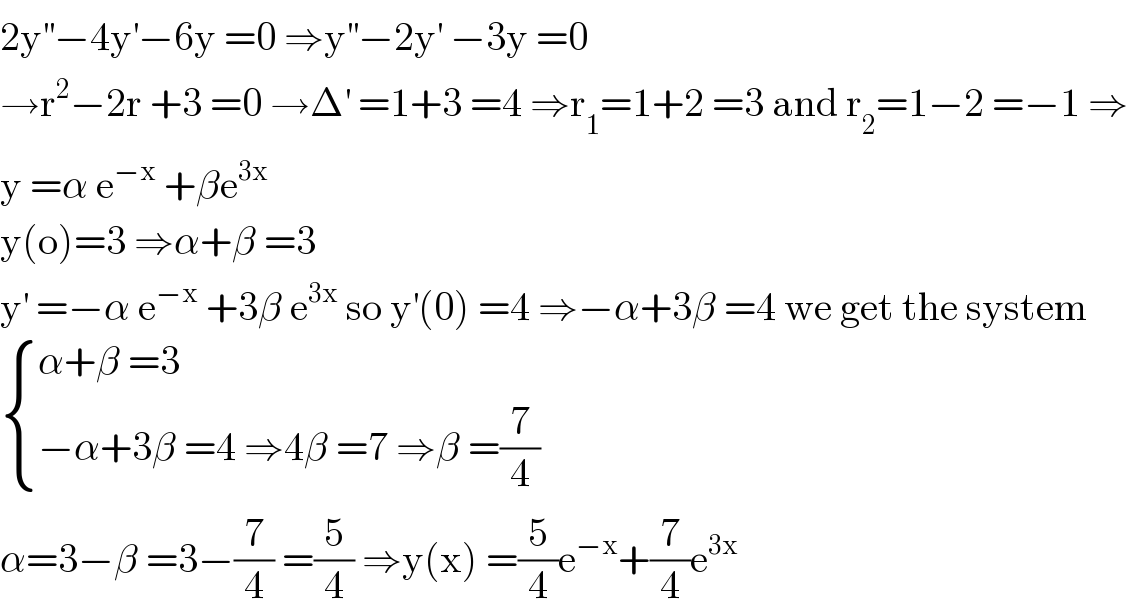
2y^(′′) −4y^′ −6y =0 ⇒y^(′′) −2y^′ −3y =0 →r^2 −2r +3 =0 →Δ^′ =1+3 =4 ⇒r_1 =1+2 =3 and r_2 =1−2 =−1 ⇒ y =α e^(−x) +βe^(3x) y(o)=3 ⇒α+β =3 y^′ =−α e^(−x) +3β e^(3x) so y^′ (0) =4 ⇒−α+3β =4 we get the system { ((α+β =3)),((−α+3β =4 ⇒4β =7 ⇒β =(7/4))) :} α=3−β =3−(7/4) =(5/4) ⇒y(x) =(5/4)e^(−x) +(7/4)e^(3x)

$$\mathrm{2y}^{''} −\mathrm{4y}^{'} −\mathrm{6y}\:=\mathrm{0}\:\Rightarrow\mathrm{y}^{''} −\mathrm{2y}^{'} \:−\mathrm{3y}\:=\mathrm{0} \\ $$$$\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{2r}\:+\mathrm{3}\:=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{1}+\mathrm{3}\:=\mathrm{4}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\mathrm{1}+\mathrm{2}\:=\mathrm{3}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\mathrm{1}−\mathrm{2}\:=−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{y}\:=\alpha\:\mathrm{e}^{−\mathrm{x}} \:+\beta\mathrm{e}^{\mathrm{3x}} \\ $$$$\mathrm{y}\left(\mathrm{o}\right)=\mathrm{3}\:\Rightarrow\alpha+\beta\:=\mathrm{3} \\ $$$$\mathrm{y}^{'} \:=−\alpha\:\mathrm{e}^{−\mathrm{x}} \:+\mathrm{3}\beta\:\mathrm{e}^{\mathrm{3x}} \:\mathrm{so}\:\mathrm{y}^{'} \left(\mathrm{0}\right)\:=\mathrm{4}\:\Rightarrow−\alpha+\mathrm{3}\beta\:=\mathrm{4}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{system} \\ $$$$\begin{cases}{\alpha+\beta\:=\mathrm{3}}\\{−\alpha+\mathrm{3}\beta\:=\mathrm{4}\:\Rightarrow\mathrm{4}\beta\:=\mathrm{7}\:\Rightarrow\beta\:=\frac{\mathrm{7}}{\mathrm{4}}}\end{cases} \\ $$$$\alpha=\mathrm{3}−\beta\:=\mathrm{3}−\frac{\mathrm{7}}{\mathrm{4}}\:=\frac{\mathrm{5}}{\mathrm{4}}\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\frac{\mathrm{5}}{\mathrm{4}}\mathrm{e}^{−\mathrm{x}} +\frac{\mathrm{7}}{\mathrm{4}}\mathrm{e}^{\mathrm{3x}} \\ $$

Answered by bobhans last updated on 16/Jul/20

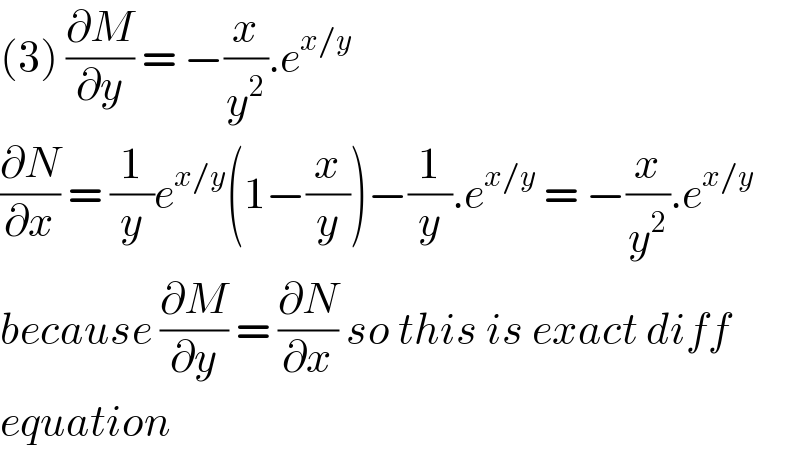
(3) (∂M/∂y) = −(x/y^2 ).e^(x/y) (∂N/∂x) = (1/y)e^(x/y) (1−(x/y))−(1/y).e^(x/y) = −(x/y^2 ).e^(x/y) because (∂M/∂y) = (∂N/∂x) so this is exact diff equation

$$\left(\mathrm{3}\right)\:\frac{\partial{M}}{\partial{y}}\:=\:−\frac{{x}}{{y}^{\mathrm{2}} }.{e}^{{x}/{y}} \:\: \\ $$$$\frac{\partial{N}}{\partial{x}}\:=\:\frac{\mathrm{1}}{{y}}{e}^{{x}/{y}} \left(\mathrm{1}−\frac{{x}}{{y}}\right)−\frac{\mathrm{1}}{{y}}.{e}^{{x}/{y}} \:=\:−\frac{{x}}{{y}^{\mathrm{2}} }.{e}^{{x}/{y}} \\ $$$${because}\:\frac{\partial{M}}{\partial{y}}\:=\:\frac{\partial{N}}{\partial{x}}\:{so}\:{this}\:{is}\:{exact}\:{diff} \\ $$$${equation} \\ $$

Commented by byaw last updated on 16/Jul/20

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{soo}\:\mathrm{much}. \\ $$

Answered by Dwaipayan Shikari last updated on 16/Jul/20

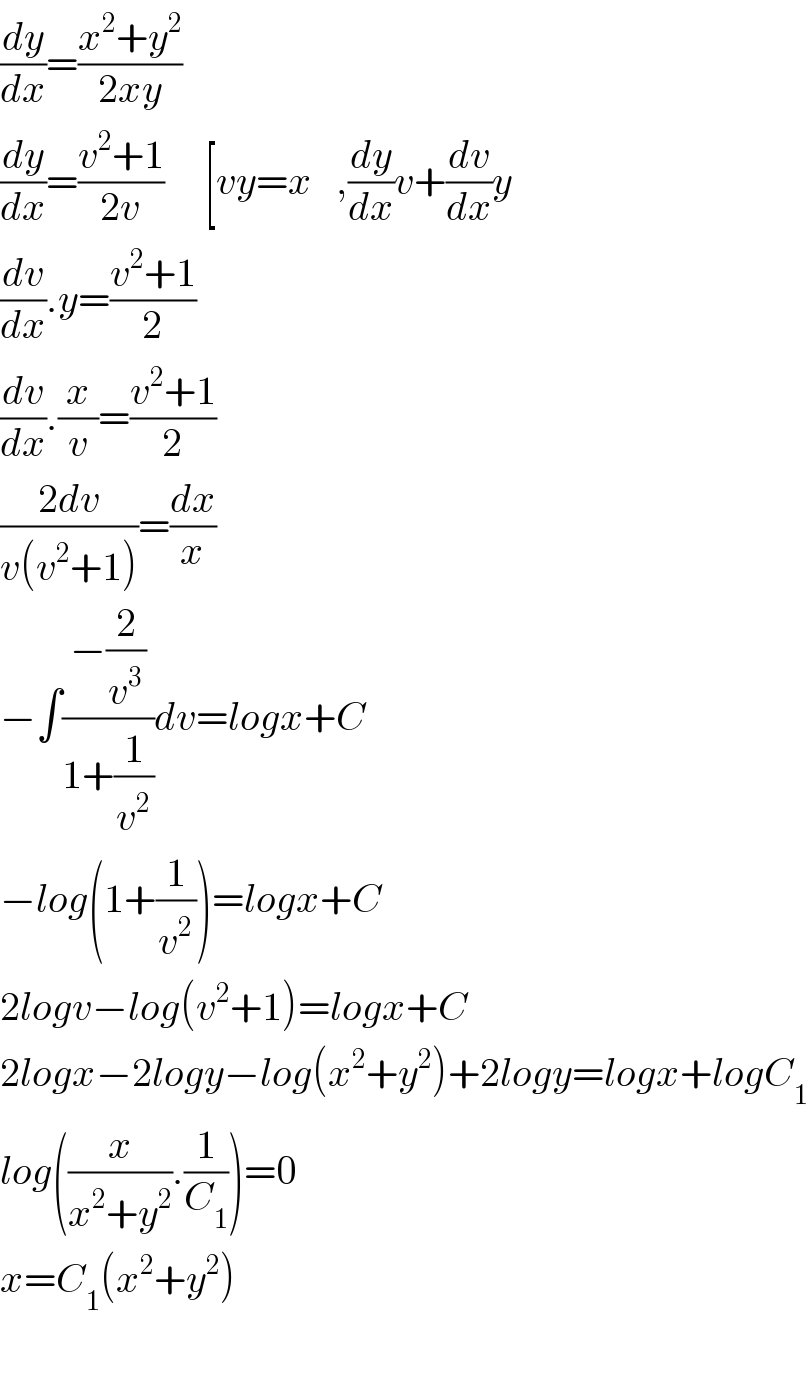
(dy/dx)=((x^2 +y^2 )/(2xy)) (dy/dx)=((v^2 +1)/(2v)) [vy=x ,(dy/dx)v+(dv/dx)y (dv/dx).y=((v^2 +1)/2) (dv/dx).(x/v)=((v^2 +1)/2) ((2dv)/(v(v^2 +1)))=(dx/x) −∫((−(2/v^3 ))/(1+(1/v^2 )))dv=logx+C −log(1+(1/v^2 ))=logx+C 2logv−log(v^2 +1)=logx+C 2logx−2logy−log(x^2 +y^2 )+2logy=logx+logC_1 log((x/(x^2 +y^2 )).(1/C_1 ))=0 x=C_1 (x^2 +y^2 )

$$\frac{{dy}}{{dx}}=\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}{xy}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{v}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{v}}\:\:\:\:\:\left[{vy}={x}\:\:\:,\frac{{dy}}{{dx}}{v}+\frac{{dv}}{{dx}}{y}\right. \\ $$$$\frac{{dv}}{{dx}}.{y}=\frac{{v}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{dv}}{{dx}}.\frac{{x}}{{v}}=\frac{{v}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{2}{dv}}{{v}\left({v}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{{dx}}{{x}} \\ $$$$−\int\frac{−\frac{\mathrm{2}}{{v}^{\mathrm{3}} }}{\mathrm{1}+\frac{\mathrm{1}}{{v}^{\mathrm{2}} }}{dv}={logx}+{C} \\ $$$$−{log}\left(\mathrm{1}+\frac{\mathrm{1}}{{v}^{\mathrm{2}} }\right)={logx}+{C} \\ $$$$\mathrm{2}{logv}−{log}\left({v}^{\mathrm{2}} +\mathrm{1}\right)={logx}+{C} \\ $$$$\mathrm{2}{logx}−\mathrm{2}{logy}−{log}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)+\mathrm{2}{logy}={logx}+{logC}_{\mathrm{1}} \\ $$$${log}\left(\frac{{x}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }.\frac{\mathrm{1}}{{C}_{\mathrm{1}} }\right)=\mathrm{0} \\ $$$${x}={C}_{\mathrm{1}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$$$ \\ $$

Commented by byaw last updated on 16/Jul/20

$$\mathrm{Thank}\:\mathrm{you}.\:\mathrm{I}\:\mathrm{am}\:\mathrm{greatful} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply