Question Number 103582 by aurpeyz last updated on 15/Jul/20

Commented by mr W last updated on 16/Jul/20
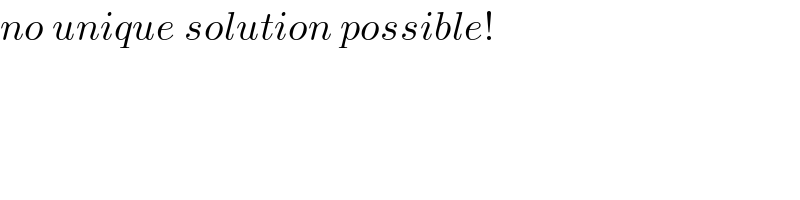
$${no}\:{unique}\:{solution}\:{possible}! \\ $$
Commented by mr W last updated on 16/Jul/20
Commented by mr W last updated on 16/Jul/20
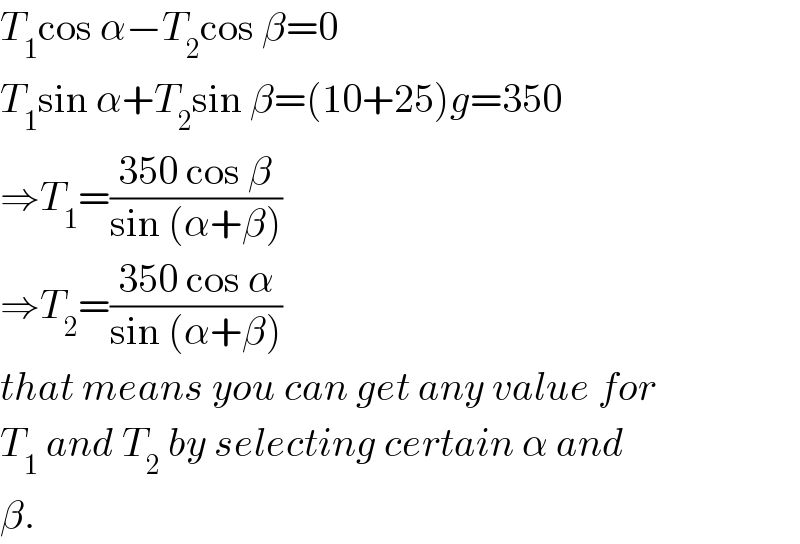
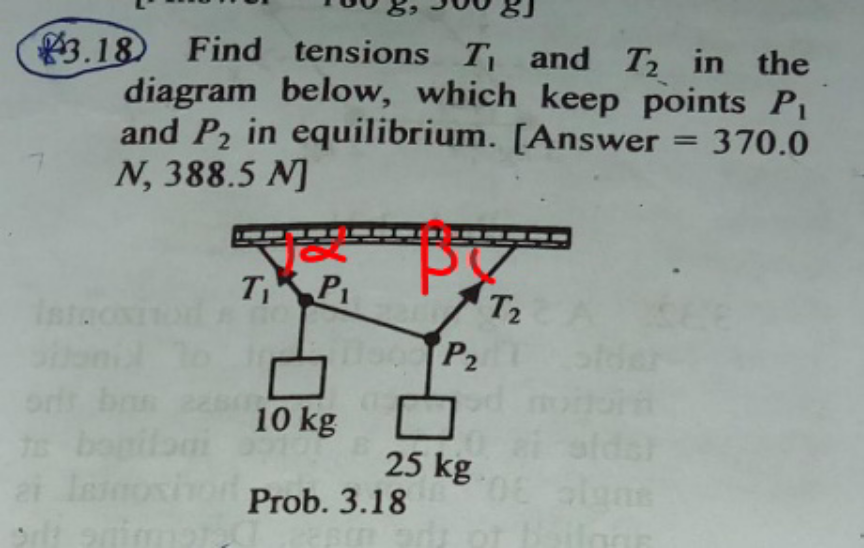
$${T}_{\mathrm{1}} \mathrm{cos}\:\alpha−{T}_{\mathrm{2}} \mathrm{cos}\:\beta=\mathrm{0} \\ $$$${T}_{\mathrm{1}} \mathrm{sin}\:\alpha+{T}_{\mathrm{2}} \mathrm{sin}\:\beta=\left(\mathrm{10}+\mathrm{25}\right){g}=\mathrm{350} \\ $$$$\Rightarrow{T}_{\mathrm{1}} =\frac{\mathrm{350}\:\mathrm{cos}\:\beta}{\mathrm{sin}\:\left(\alpha+\beta\right)} \\ $$$$\Rightarrow{T}_{\mathrm{2}} =\frac{\mathrm{350}\:\mathrm{cos}\:\alpha}{\mathrm{sin}\:\left(\alpha+\beta\right)} \\ $$$${that}\:{means}\:{you}\:{can}\:{get}\:{any}\:{value}\:{for} \\ $$$${T}_{\mathrm{1}} \:{and}\:{T}_{\mathrm{2}} \:{by}\:{selecting}\:{certain}\:\alpha\:{and} \\ $$$$\beta. \\ $$
