Question Number 103586 by aurpeyz last updated on 15/Jul/20

Answered by OlafThorendsen last updated on 16/Jul/20
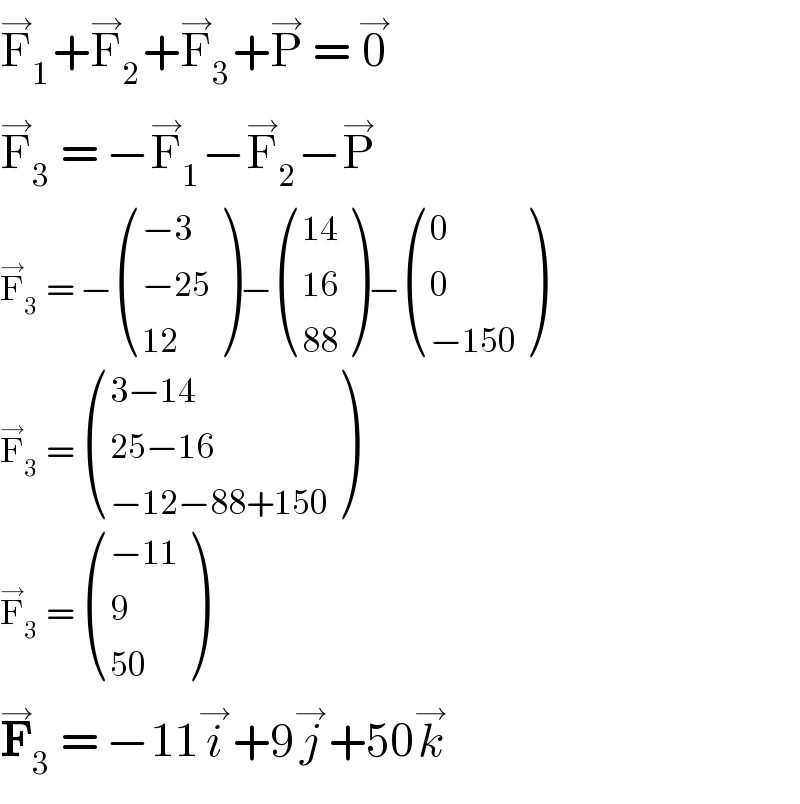
$$\overset{\rightarrow} {\mathrm{F}}_{\mathrm{1}} +\overset{\rightarrow} {\mathrm{F}}_{\mathrm{2}} +\overset{\rightarrow} {\mathrm{F}}_{\mathrm{3}} +\overset{\rightarrow} {\mathrm{P}}\:=\:\overset{\rightarrow} {\mathrm{0}} \\ $$$$\overset{\rightarrow} {\mathrm{F}}_{\mathrm{3}} \:=\:−\overset{\rightarrow} {\mathrm{F}}_{\mathrm{1}} −\overset{\rightarrow} {\mathrm{F}}_{\mathrm{2}} −\overset{\rightarrow} {\mathrm{P}} \\ $$$$\overset{\rightarrow} {\mathrm{F}}_{\mathrm{3}} \:=\:−\begin{pmatrix}{−\mathrm{3}}\\{−\mathrm{25}}\\{\mathrm{12}}\end{pmatrix}−\begin{pmatrix}{\mathrm{14}}\\{\mathrm{16}}\\{\mathrm{88}}\end{pmatrix}−\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\\{−\mathrm{150}}\end{pmatrix} \\ $$$$\overset{\rightarrow} {\mathrm{F}}_{\mathrm{3}} \:=\:\begin{pmatrix}{\mathrm{3}−\mathrm{14}}\\{\mathrm{25}−\mathrm{16}}\\{−\mathrm{12}−\mathrm{88}+\mathrm{150}}\end{pmatrix} \\ $$$$\overset{\rightarrow} {\mathrm{F}}_{\mathrm{3}} \:=\:\begin{pmatrix}{−\mathrm{11}}\\{\mathrm{9}}\\{\mathrm{50}}\end{pmatrix} \\ $$$$\overset{\rightarrow} {\boldsymbol{\mathrm{F}}}_{\mathrm{3}} \:=\:−\mathrm{11}\overset{\rightarrow} {{i}}+\mathrm{9}\overset{\rightarrow} {{j}}+\mathrm{50}\overset{\rightarrow} {{k}} \\ $$
