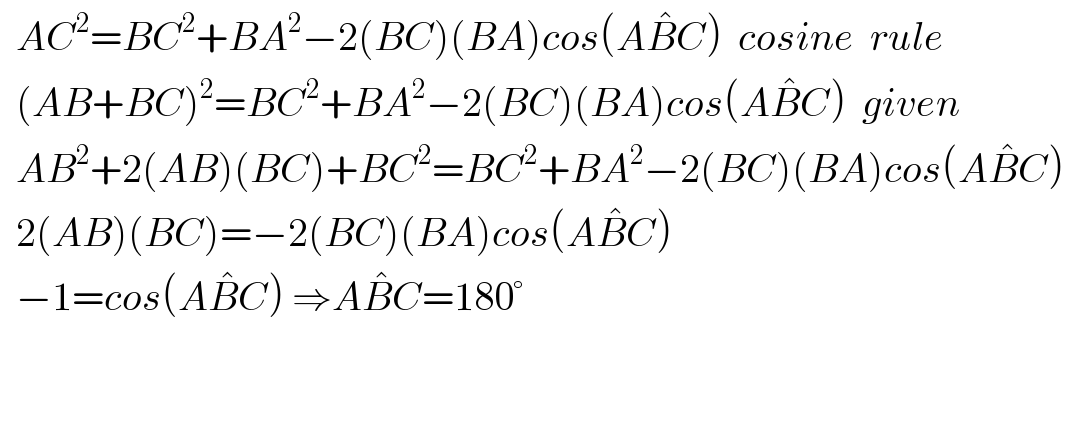Question-103672

Question Number 103672 by M±th+et+s last updated on 16/Jul/20

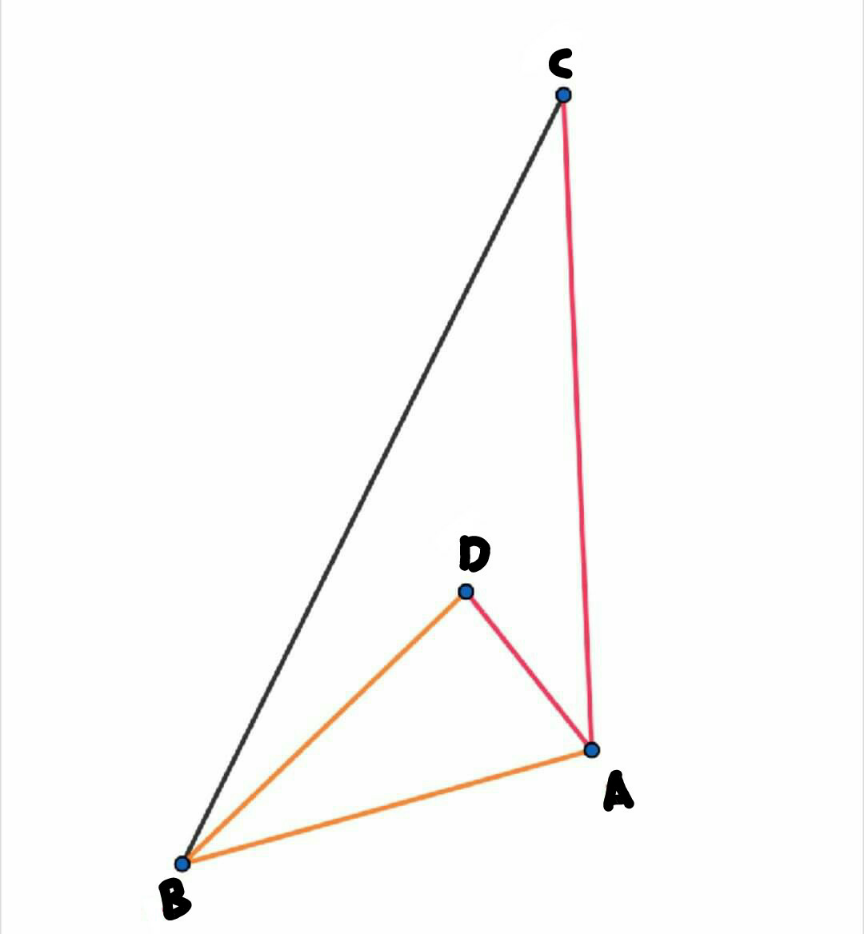
Commented by M±th+et+s last updated on 16/Jul/20

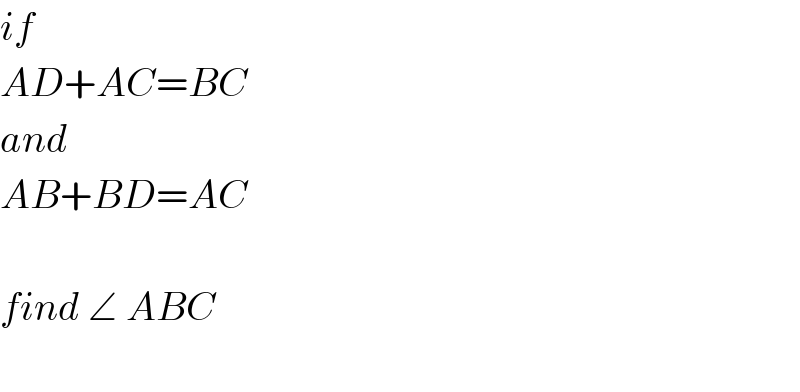
i f

A D + A C = B C

a n d

A B + B D = A C

f i n d ∠ A B C

Commented by som(math1967) last updated on 16/Jul/20

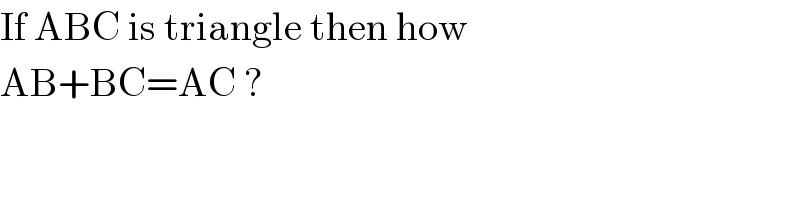
If ABC is triangle then how

AB + BC = AC ?

Commented by M±th+et+s last updated on 16/Jul/20

s o r r y s i r i t s t y p o

t h a n k y o u f o r y o u r c o m m e n t

Answered by Worm_Tail last updated on 16/Jul/20

{A C}^{2} = {B C}^{2} + {B A}^{2} - 2 (B C) (B A) c o s (A \hat{B C}) c o s i n e r u l e

{(A B + B C)}^{2} = {B C}^{2} + {B A}^{2} - 2 (B C) (B A) c o s (A \hat{B C}) g i v e n

{A B}^{2} + 2 (A B) (B C) + {B C}^{2} = {B C}^{2} + {B A}^{2} - 2 (B C) (B A) c o s (A \hat{B C})

2 (A B) (B C) = - 2 (B C) (B A) c o s (A \hat{B C})

- 1 = c o s (A \hat{B C}) \Rightarrow A \hat{B C} = 180 °