Question Number 103700 by anonymous last updated on 16/Jul/20

Commented by anonymous last updated on 16/Jul/20

$${plzz}\:{help}\:{me} \\ $$
Answered by bobhans last updated on 17/Jul/20
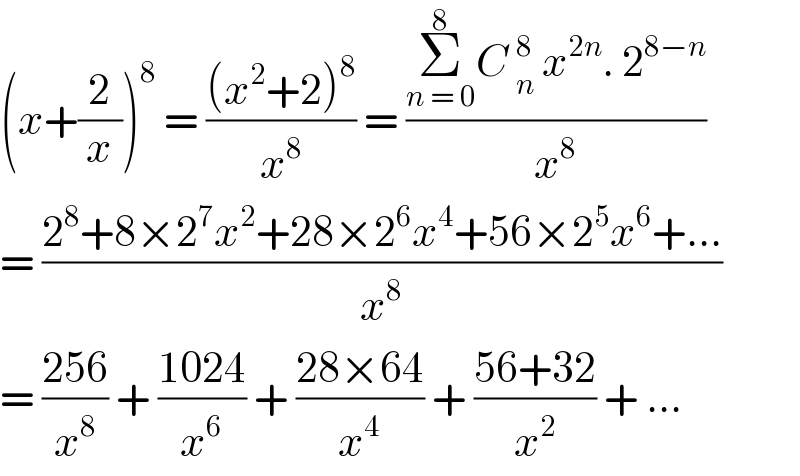
$$\left({x}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{8}} \:=\:\frac{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{8}} }{{x}^{\mathrm{8}} }\:=\:\frac{\underset{{n}\:=\:\mathrm{0}} {\overset{\mathrm{8}} {\sum}}{C}\:_{{n}} ^{\mathrm{8}} \:{x}^{\mathrm{2}{n}} .\:\mathrm{2}^{\mathrm{8}−{n}} }{{x}^{\mathrm{8}} } \\ $$$$=\:\frac{\mathrm{2}^{\mathrm{8}} +\mathrm{8}×\mathrm{2}^{\mathrm{7}} {x}^{\mathrm{2}} +\mathrm{28}×\mathrm{2}^{\mathrm{6}} {x}^{\mathrm{4}} +\mathrm{56}×\mathrm{2}^{\mathrm{5}} {x}^{\mathrm{6}} +…}{{x}^{\mathrm{8}} } \\ $$$$=\:\frac{\mathrm{256}}{{x}^{\mathrm{8}} }\:+\:\frac{\mathrm{1024}}{{x}^{\mathrm{6}} }\:+\:\frac{\mathrm{28}×\mathrm{64}}{{x}^{\mathrm{4}} }\:+\:\frac{\mathrm{56}+\mathrm{32}}{{x}^{\mathrm{2}} }\:+\:…\: \\ $$
