Question Number 103756 by ajfour last updated on 17/Jul/20

Commented by ajfour last updated on 17/Jul/20
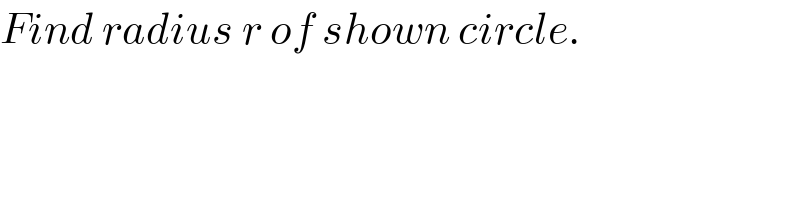
$${Find}\:{radius}\:{r}\:{of}\:{shown}\:{circle}. \\ $$
Answered by mr W last updated on 17/Jul/20
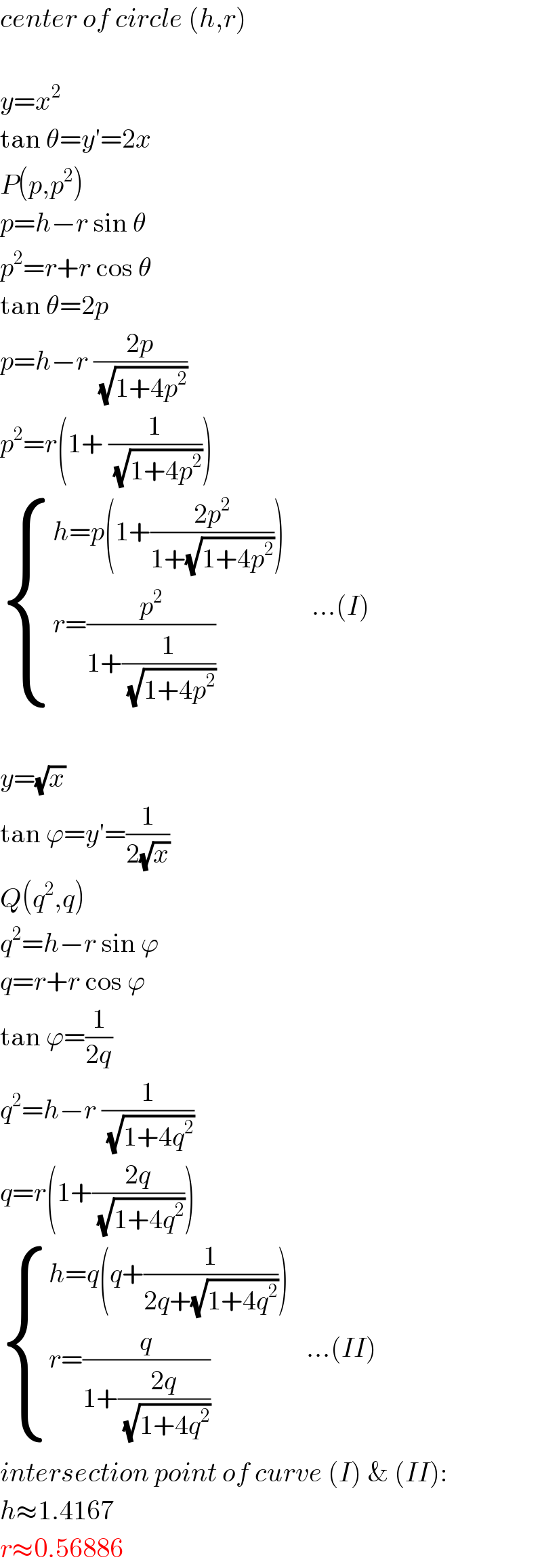
$${center}\:{of}\:{circle}\:\left({h},{r}\right) \\ $$$$ \\ $$$${y}={x}^{\mathrm{2}} \\ $$$$\mathrm{tan}\:\theta={y}'=\mathrm{2}{x} \\ $$$${P}\left({p},{p}^{\mathrm{2}} \right) \\ $$$${p}={h}−{r}\:\mathrm{sin}\:\theta \\ $$$${p}^{\mathrm{2}} ={r}+{r}\:\mathrm{cos}\:\theta \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}{p} \\ $$$${p}={h}−{r}\:\frac{\mathrm{2}{p}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }} \\ $$$${p}^{\mathrm{2}} ={r}\left(\mathrm{1}+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}\right) \\ $$$$\begin{cases}{{h}={p}\left(\mathrm{1}+\frac{\mathrm{2}{p}^{\mathrm{2}} }{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}\right)}\\{{r}=\frac{{p}^{\mathrm{2}} }{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}}}\end{cases}\:\:\:\:\:…\left({I}\right) \\ $$$$ \\ $$$${y}=\sqrt{{x}} \\ $$$$\mathrm{tan}\:\varphi={y}'=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}} \\ $$$${Q}\left({q}^{\mathrm{2}} ,{q}\right) \\ $$$${q}^{\mathrm{2}} ={h}−{r}\:\mathrm{sin}\:\varphi \\ $$$${q}={r}+{r}\:\mathrm{cos}\:\varphi \\ $$$$\mathrm{tan}\:\varphi=\frac{\mathrm{1}}{\mathrm{2}{q}} \\ $$$${q}^{\mathrm{2}} ={h}−{r}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{q}^{\mathrm{2}} }} \\ $$$${q}={r}\left(\mathrm{1}+\frac{\mathrm{2}{q}}{\:\sqrt{\mathrm{1}+\mathrm{4}{q}^{\mathrm{2}} }}\right) \\ $$$$\begin{cases}{{h}={q}\left({q}+\frac{\mathrm{1}}{\mathrm{2}{q}+\sqrt{\mathrm{1}+\mathrm{4}{q}^{\mathrm{2}} }}\right)}\\{{r}=\frac{{q}}{\mathrm{1}+\frac{\mathrm{2}{q}}{\:\sqrt{\mathrm{1}+\mathrm{4}{q}^{\mathrm{2}} }}}}\end{cases}\:\:\:…\left({II}\right) \\ $$$${intersection}\:{point}\:{of}\:{curve}\:\left({I}\right)\:\&\:\left({II}\right): \\ $$$${h}\approx\mathrm{1}.\mathrm{4167} \\ $$$${r}\approx\mathrm{0}.\mathrm{56886} \\ $$
Commented by mr W last updated on 17/Jul/20

Commented by mr W last updated on 17/Jul/20

Commented by ajfour last updated on 17/Jul/20
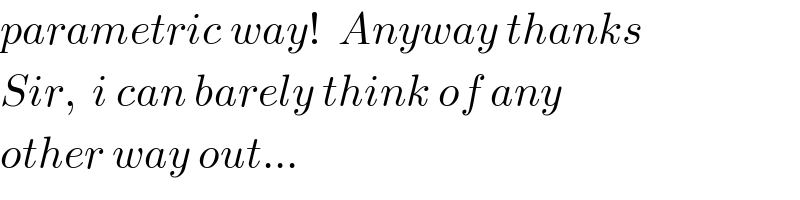
$${parametric}\:{way}!\:\:{Anyway}\:{thanks} \\ $$$${Sir},\:\:{i}\:{can}\:{barely}\:{think}\:{of}\:{any} \\ $$$${other}\:{way}\:{out}… \\ $$
