Question Number 103774 by dw last updated on 17/Jul/20
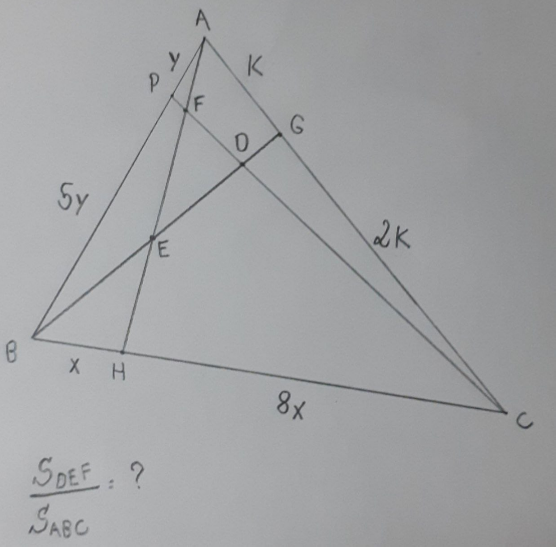
Answered by mr W last updated on 17/Jul/20
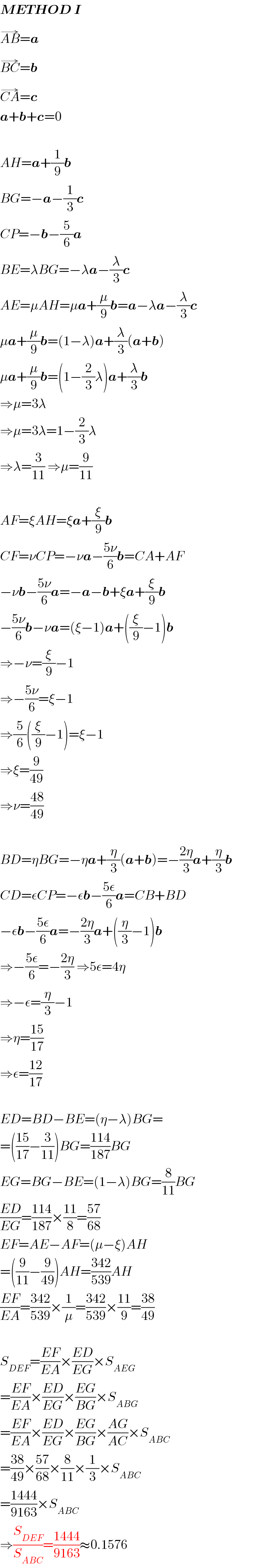
$$\boldsymbol{{METHOD}}\:\boldsymbol{{I}} \\ $$$$\overset{\rightarrow} {{AB}}=\boldsymbol{{a}} \\ $$$$\overset{\rightarrow} {{BC}}=\boldsymbol{{b}} \\ $$$$\overset{\rightarrow} {{CA}}=\boldsymbol{{c}} \\ $$$$\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}=\mathrm{0} \\ $$$$ \\ $$$${AH}=\boldsymbol{{a}}+\frac{\mathrm{1}}{\mathrm{9}}\boldsymbol{{b}} \\ $$$${BG}=−\boldsymbol{{a}}−\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{{c}} \\ $$$${CP}=−\boldsymbol{{b}}−\frac{\mathrm{5}}{\mathrm{6}}\boldsymbol{{a}} \\ $$$${BE}=\lambda{BG}=−\lambda\boldsymbol{{a}}−\frac{\lambda}{\mathrm{3}}\boldsymbol{{c}} \\ $$$${AE}=\mu{AH}=\mu\boldsymbol{{a}}+\frac{\mu}{\mathrm{9}}\boldsymbol{{b}}=\boldsymbol{{a}}−\lambda\boldsymbol{{a}}−\frac{\lambda}{\mathrm{3}}\boldsymbol{{c}} \\ $$$$\mu\boldsymbol{{a}}+\frac{\mu}{\mathrm{9}}\boldsymbol{{b}}=\left(\mathrm{1}−\lambda\right)\boldsymbol{{a}}+\frac{\lambda}{\mathrm{3}}\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right) \\ $$$$\mu\boldsymbol{{a}}+\frac{\mu}{\mathrm{9}}\boldsymbol{{b}}=\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\lambda\right)\boldsymbol{{a}}+\frac{\lambda}{\mathrm{3}}\boldsymbol{{b}} \\ $$$$\Rightarrow\mu=\mathrm{3}\lambda \\ $$$$\Rightarrow\mu=\mathrm{3}\lambda=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\lambda \\ $$$$\Rightarrow\lambda=\frac{\mathrm{3}}{\mathrm{11}}\:\Rightarrow\mu=\frac{\mathrm{9}}{\mathrm{11}} \\ $$$$ \\ $$$${AF}=\xi{AH}=\xi\boldsymbol{{a}}+\frac{\xi}{\mathrm{9}}\boldsymbol{{b}} \\ $$$${CF}=\nu{CP}=−\nu\boldsymbol{{a}}−\frac{\mathrm{5}\nu}{\mathrm{6}}\boldsymbol{{b}}={CA}+{AF} \\ $$$$−\nu\boldsymbol{{b}}−\frac{\mathrm{5}\nu}{\mathrm{6}}\boldsymbol{{a}}=−\boldsymbol{{a}}−\boldsymbol{{b}}+\xi\boldsymbol{{a}}+\frac{\xi}{\mathrm{9}}\boldsymbol{{b}} \\ $$$$−\frac{\mathrm{5}\nu}{\mathrm{6}}\boldsymbol{{b}}−\nu\boldsymbol{{a}}=\left(\xi−\mathrm{1}\right)\boldsymbol{{a}}+\left(\frac{\xi}{\mathrm{9}}−\mathrm{1}\right)\boldsymbol{{b}} \\ $$$$\Rightarrow−\nu=\frac{\xi}{\mathrm{9}}−\mathrm{1} \\ $$$$\Rightarrow−\frac{\mathrm{5}\nu}{\mathrm{6}}=\xi−\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{5}}{\mathrm{6}}\left(\frac{\xi}{\mathrm{9}}−\mathrm{1}\right)=\xi−\mathrm{1} \\ $$$$\Rightarrow\xi=\frac{\mathrm{9}}{\mathrm{49}} \\ $$$$\Rightarrow\nu=\frac{\mathrm{48}}{\mathrm{49}} \\ $$$$ \\ $$$${BD}=\eta{BG}=−\eta\boldsymbol{{a}}+\frac{\eta}{\mathrm{3}}\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)=−\frac{\mathrm{2}\eta}{\mathrm{3}}\boldsymbol{{a}}+\frac{\eta}{\mathrm{3}}\boldsymbol{{b}} \\ $$$${CD}=\epsilon{CP}=−\epsilon\boldsymbol{{b}}−\frac{\mathrm{5}\epsilon}{\mathrm{6}}\boldsymbol{{a}}={CB}+{BD} \\ $$$$−\epsilon\boldsymbol{{b}}−\frac{\mathrm{5}\epsilon}{\mathrm{6}}\boldsymbol{{a}}=−\frac{\mathrm{2}\eta}{\mathrm{3}}\boldsymbol{{a}}+\left(\frac{\eta}{\mathrm{3}}−\mathrm{1}\right)\boldsymbol{{b}} \\ $$$$\Rightarrow−\frac{\mathrm{5}\epsilon}{\mathrm{6}}=−\frac{\mathrm{2}\eta}{\mathrm{3}}\:\Rightarrow\mathrm{5}\epsilon=\mathrm{4}\eta \\ $$$$\Rightarrow−\epsilon=\frac{\eta}{\mathrm{3}}−\mathrm{1} \\ $$$$\Rightarrow\eta=\frac{\mathrm{15}}{\mathrm{17}} \\ $$$$\Rightarrow\epsilon=\frac{\mathrm{12}}{\mathrm{17}} \\ $$$$ \\ $$$${ED}={BD}−{BE}=\left(\eta−\lambda\right){BG}= \\ $$$$=\left(\frac{\mathrm{15}}{\mathrm{17}}−\frac{\mathrm{3}}{\mathrm{11}}\right){BG}=\frac{\mathrm{114}}{\mathrm{187}}{BG} \\ $$$${EG}={BG}−{BE}=\left(\mathrm{1}−\lambda\right){BG}=\frac{\mathrm{8}}{\mathrm{11}}{BG} \\ $$$$\frac{{ED}}{{EG}}=\frac{\mathrm{114}}{\mathrm{187}}×\frac{\mathrm{11}}{\mathrm{8}}=\frac{\mathrm{57}}{\mathrm{68}} \\ $$$${EF}={AE}−{AF}=\left(\mu−\xi\right){AH} \\ $$$$=\left(\frac{\mathrm{9}}{\mathrm{11}}−\frac{\mathrm{9}}{\mathrm{49}}\right){AH}=\frac{\mathrm{342}}{\mathrm{539}}{AH} \\ $$$$\frac{{EF}}{{EA}}=\frac{\mathrm{342}}{\mathrm{539}}×\frac{\mathrm{1}}{\mu}=\frac{\mathrm{342}}{\mathrm{539}}×\frac{\mathrm{11}}{\mathrm{9}}=\frac{\mathrm{38}}{\mathrm{49}} \\ $$$$ \\ $$$${S}_{{DEF}} =\frac{{EF}}{{EA}}×\frac{{ED}}{{EG}}×{S}_{{AEG}} \\ $$$$=\frac{{EF}}{{EA}}×\frac{{ED}}{{EG}}×\frac{{EG}}{{BG}}×{S}_{{ABG}} \\ $$$$=\frac{{EF}}{{EA}}×\frac{{ED}}{{EG}}×\frac{{EG}}{{BG}}×\frac{{AG}}{{AC}}×{S}_{{ABC}} \\ $$$$=\frac{\mathrm{38}}{\mathrm{49}}×\frac{\mathrm{57}}{\mathrm{68}}×\frac{\mathrm{8}}{\mathrm{11}}×\frac{\mathrm{1}}{\mathrm{3}}×{S}_{{ABC}} \\ $$$$=\frac{\mathrm{1444}}{\mathrm{9163}}×{S}_{{ABC}} \\ $$$$\Rightarrow\frac{{S}_{{DEF}} }{{S}_{{ABC}} }=\frac{\mathrm{1444}}{\mathrm{9163}}\approx\mathrm{0}.\mathrm{1576} \\ $$
