Question Number 103790 by ugwu Kingsley last updated on 17/Jul/20

Commented by ugwu Kingsley last updated on 17/Jul/20
$${i}\:{need}\:{help}\:{with}\:{this}\:{asap} \\ $$
Answered by bemath last updated on 17/Jul/20
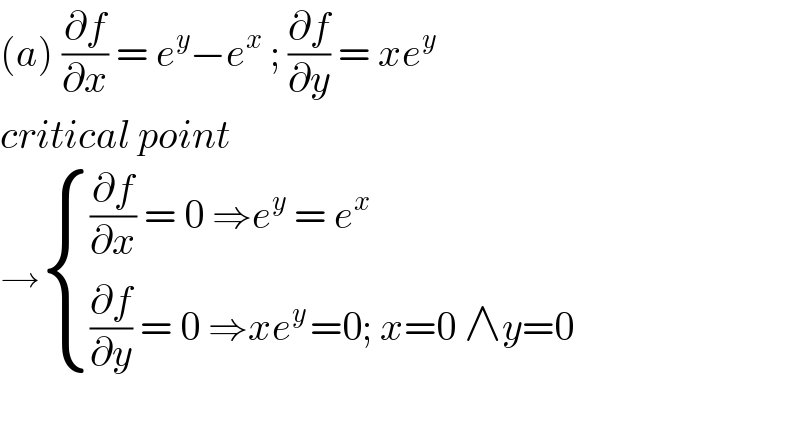
$$\left({a}\right)\:\frac{\partial{f}}{\partial{x}}\:=\:{e}^{{y}} −{e}^{{x}} \:;\:\frac{\partial{f}}{\partial{y}}\:=\:{xe}^{{y}} \\ $$$${critical}\:{point} \\ $$$$\rightarrow\begin{cases}{\frac{\partial{f}}{\partial{x}}\:=\:\mathrm{0}\:\Rightarrow{e}^{{y}} \:=\:{e}^{{x}} }\\{\frac{\partial{f}}{\partial{y}}\:=\:\mathrm{0}\:\Rightarrow{xe}^{{y}\:} =\mathrm{0};\:{x}=\mathrm{0}\:\wedge{y}=\mathrm{0}}\end{cases} \\ $$$$ \\ $$
Commented by bemath last updated on 17/Jul/20
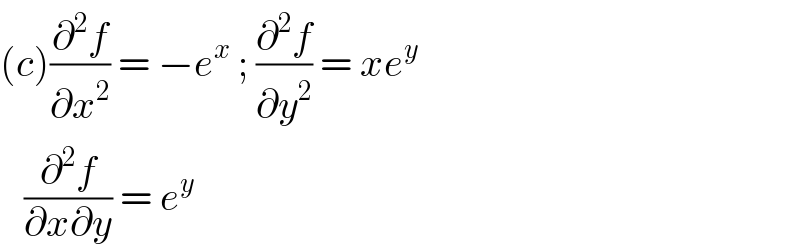
$$\left({c}\right)\frac{\partial^{\mathrm{2}} {f}}{\partial{x}^{\mathrm{2}} }\:=\:−{e}^{{x}} \:;\:\frac{\partial^{\mathrm{2}} {f}}{\partial{y}^{\mathrm{2}} }\:=\:{xe}^{{y}} \\ $$$$\:\:\:\frac{\partial^{\mathrm{2}} {f}}{\partial{x}\partial{y}}\:=\:{e}^{{y}} \: \\ $$
