Question Number 103872 by mikolo last updated on 17/Jul/20

Commented by bramlex last updated on 18/Jul/20

Commented by bramlex last updated on 18/Jul/20
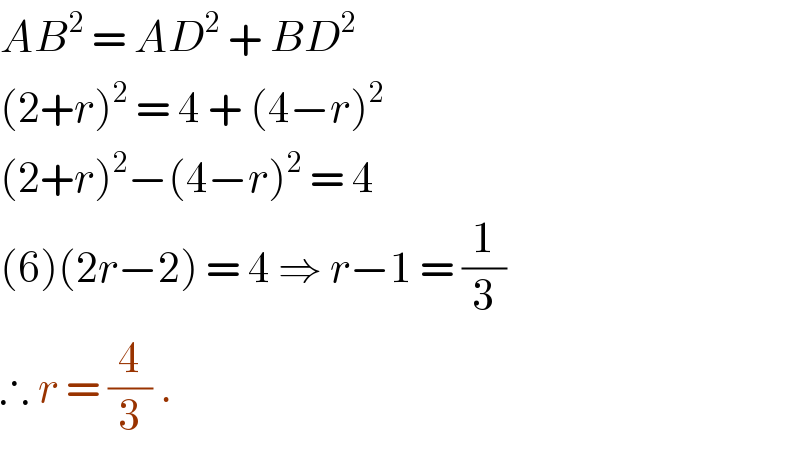
$${AB}^{\mathrm{2}} \:=\:{AD}^{\mathrm{2}} \:+\:{BD}^{\mathrm{2}} \\ $$$$\left(\mathrm{2}+{r}\right)^{\mathrm{2}} \:=\:\mathrm{4}\:+\:\left(\mathrm{4}−{r}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{2}+{r}\right)^{\mathrm{2}} −\left(\mathrm{4}−{r}\right)^{\mathrm{2}} \:=\:\mathrm{4} \\ $$$$\left(\mathrm{6}\right)\left(\mathrm{2}{r}−\mathrm{2}\right)\:=\:\mathrm{4}\:\Rightarrow\:{r}−\mathrm{1}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\therefore\:{r}\:=\:\frac{\mathrm{4}}{\mathrm{3}}\:. \\ $$
Commented by bramlex last updated on 18/Jul/20
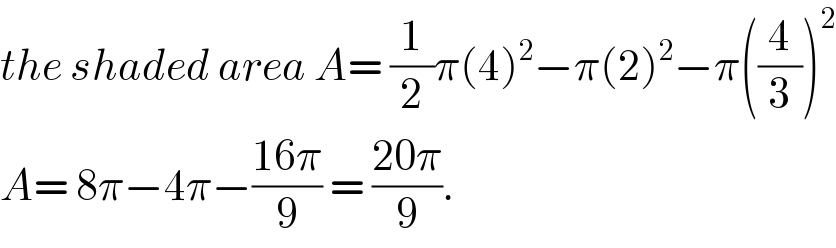
$${the}\:{shaded}\:{area}\:{A}=\:\frac{\mathrm{1}}{\mathrm{2}}\pi\left(\mathrm{4}\right)^{\mathrm{2}} −\pi\left(\mathrm{2}\right)^{\mathrm{2}} −\pi\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$${A}=\:\mathrm{8}\pi−\mathrm{4}\pi−\frac{\mathrm{16}\pi}{\mathrm{9}}\:=\:\frac{\mathrm{20}\pi}{\mathrm{9}}.\: \\ $$
