Question Number 104071 by DGmichael last updated on 19/Jul/20

Answered by Dwaipayan Shikari last updated on 19/Jul/20
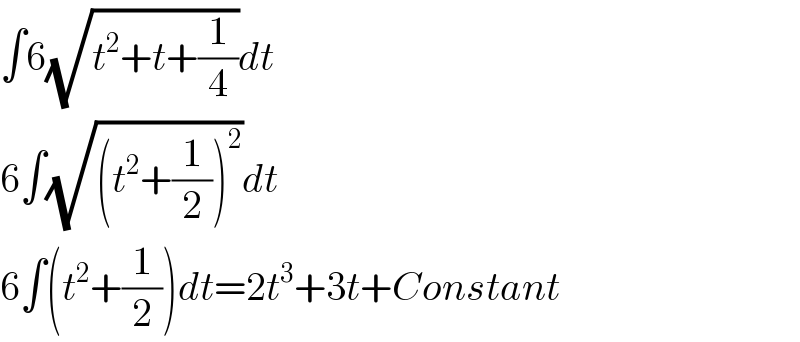
$$\int\mathrm{6}\sqrt{{t}^{\mathrm{2}} +{t}+\frac{\mathrm{1}}{\mathrm{4}}}{dt} \\ $$$$\mathrm{6}\int\sqrt{\left({t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{dt} \\ $$$$\mathrm{6}\int\left({t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right){dt}=\mathrm{2}{t}^{\mathrm{3}} +\mathrm{3}{t}+{Constant} \\ $$
Answered by bobhans last updated on 19/Jul/20

$$\mathrm{36}{t}^{\mathrm{4}} +\mathrm{36}{t}^{\mathrm{2}} +\mathrm{9}\:=\:\left(\mathrm{6}{t}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} >\:\mathrm{0}\:,\forall{t}\in\mathbb{R} \\ $$$$\int\:\sqrt{\left(\mathrm{6}{t}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }\:{dt}\:=\:\mathrm{2}{t}^{\mathrm{3}} \:+\:\mathrm{3}{t}\:+\:{C} \\ $$
Commented by DGmichael last updated on 19/Jul/20
����
